Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

2. Beweise und Gegenbeweise

Räumliche Erscheinungen und ihre Deutung – Kongruente Dreiecke – Ein Widerspruch? – Das Kantsche Beispiel – Drehung im Raume – Scheinbare und wirkliche Kongruenz – Vom »Richtungssinn« der Figuren – Die Beweiskraft der Anschauung – Der Mangel der Analogie

Die bisher angeführten Argumente, die für die Möglichkeit oder das Vorhandensein einer vierten Dimension geltend gemacht werden, sind ihrer Natur nach mehr Überlegungs- und Analogiebeweise als Tatsachen der Wirklichkeit, denen letzten Endes doch die größere Beweiskraft zukommt. Man hat aber auch gewisse räumlich-geometrische Erscheinungen, die in unserer dreidimensionalen Welt zu konstatieren sind, und denen in höherem Maße als jenen der Wert von Tatsachen- und Wirklichkeitsbeweisen zuzukommen scheint, im Sinne einer vierten Dimension zu deuten gesucht. Wiederum wollen wir uns das Wesen dieser Erscheinungen zunächst durch analoge Verhältnisse der zweiten Dimension zu veranschaulichen suchen.

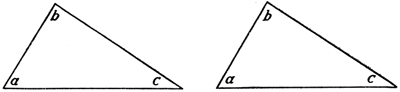
Abb. 37

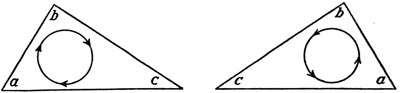
Abb. 38

In unserer Abbildung 37 sind zwei Dreiecke gezeichnet, die in Winkeln und Seiten vollkommen übereinstimmen. Solche Dreiecke werden bekanntlich als kongruent bezeichnet und haben die Eigenschaft, daß sie zu vollkommener Deckung gebracht werden können. Das geschieht bei den Dreiecken der Abbildung 37 in der Weise, daß man das eine Dreieck über das andere innerhalb der Ebene, in der sich beide befinden, hinweggeschoben denkt, bis die entsprechenden Seiten aufeinanderfallen. In der Abbildung 38 sind dieselben Dreiecke nochmals vorgeführt, diesmal jedoch nicht wie in Abbildung 37 in Parallel-, sondern in Gegen- oder Spiegelstellung; hier ist also das eine Dreieck gleichsam das Spiegelbild des anderen. Diese beiden Dreiecke nun können durch Verschiebung innerhalb der Ebene auf keine Weise zur Deckung gebracht werden, wie sich der Leser leicht überzeugen kann, wenn er die beiden Figuren ausschneidet und gegeneinander verschiebt. Obwohl also die Dreiecke der Abbildung 38 ebenfalls kongruent sind, ebenfalls in Seiten und Winkeln vollkommen übereinstimmen (es sind ja dieselben Dreiecke wie in Abbildung 37, nur in anderer Stellung), ist es doch unmöglich, diese Dreiecke ebenso wie jene anderen beiden durch bloße Verschiebung innerhalb der Ebene zur Deckung zu bringen. Nur auf eine Weise können auch diese Dreiecke zur Deckung gebracht werden, indem man nämlich eins der Dreiecke aus der Ebene herausgehoben denkt (etwa durch Ausschneiden aus dem Papier), es im dreidimensionalen Raume um seine Achse dreht und es dann so auf das andere Dreieck legt, daß die entsprechenden Seiten und Winkel aufeinanderfallen. Hier liegt also der Fall vor, daß zwei kongruente räumliche Gebilde innerhalb der Dimension, der sie selbst angehören, nicht zur Deckung gebracht werden können, daß das vielmehr nur durch Zuhilfenahme einer weiteren Dimension, in unserem Falle der dritten, möglich gemacht werden kann. Hier scheint also ein Widerspruch vorzuliegen, der Widerspruch nämlich, daß es unter denselben gegebenen Bedingungen einmal möglich, das andere Mal aber unmöglich ist, dieselben räumlichen Gebilde zur Deckung zu bringen.

Ganz ähnliche Erscheinungen wie hier in der zweidimensionalen Ebene und an zweidimensionalen geometrischen Gebilden gibt es nun auch im dreidimensionalen Raume. Es gibt Körper, die selbst bei vorhandener vollkommener Kongruenz ihrer Seiten und Winkel doch nicht zur Deckung gebracht werden können. Ein Tetraeder ist ein von vier Dreiecksseiten begrenzter Körper, ist gleichsam das dreidimensionale Gegenstück zum zweidimensionalen Dreieck. Zwei kongruente Tetraeder in Parallelstellung können jederzeit zur Deckung gebracht werden, zwei kongruente Tetraeder in Spiegelstellung dagegen, wenn sie nicht gleichzeitig symmetrisch gebaut sind, niemals. Allgemein kann ein unsymmetrischer Körper, d. h. ein Körper, der nicht in zwei kongruente Hälften geteilt werden kann, niemals mit seinem Spiegelbild zur Deckung (wenn auch nur in Gedanken) gebracht werden, obgleich natürlich jeder Körper mit seinem Spiegelbild vollkommen kongruent ist. Auf solche Erscheinungen hat schon Kant hingewiesen und die Frage aufgeworfen, ob diese im Sinne einer vierten Dimension zu deuten wären. Von ihm stammt das berühmte Beispiel der rechten und linken Hand, die, selbst wenn sie beide vollkommen gleich gebildet sind, dennoch niemals zur Deckung gebracht werden können; oder der Handschuh der einen Hand läßt sich nicht ohne Verzerrung, d. h. ohne Veränderung seiner geometrischen Form, auf die andere Hand ziehen. Hier scheint also ein Widerspruch vorzuliegen. Unser Denken verlangt, daß sich Körper, die kongruent sind, zur Deckung bringen lassen, und dennoch ist das bei solchen wie den erwähnten Körpern auf keine Weise möglich.

Diese Erscheinungen und der Widerspruch, den man in ihnen sehen zu müssen glaubte, boten die Möglichkeit einer Erklärung durch Annahme einer vierten Dimension. Wie die beiden Dreiecke in Spiegelstellung (Abbildung 38), also kongruente Figuren der zweiten Dimension, die trotz vollkommener Kongruenz von Seiten und Winkeln durch bloße Verschiebung innerhalb der zweidimensionalen Ebene nicht zur Deckung gebracht werden können, sich vermittels der dritten Dimension zur Deckung bringen lassen, so werden sich vielleicht, so folgerte man, analogiegemäß auch solche wie die erwähnten kongruenten dreidimensionalen Gebilde vermittels einer vierten Dimension zur Deckung bringen lassen. Jene kongruenten Körper müßten also gleichsam aus dem dreidimensionalen Raume heraus und in die vierte Dimension hineingebracht werden und in dieser, analog dem Vorgang mit den Dreiecken, eine Art Drehung erfahren. Wir können uns zwar von einer solchen Drehung in der vierten Dimension ebensowenig wie von einer vierten Dimension überhaupt eine Vorstellung machen, aber das allein brauchte kein Grund zu sein, eine solche Annahme abzuweisen; zweidimensionale Lebewesen könnten sich auch keine sinnfällige Vorstellung von der Drehung machen, durch welche die Dreiecke der Abbildung 38 zur Deckung gebracht werden können. Wiederum hat auch diese Analogie etwas ungemein Bestechendes; sie bietet eine überraschend einfache Erklärung jener Erscheinungen, und der in diesen Erscheinungen erblickte Widerspruch schien nunmehr geradezu ein Argument für das Vorhandensein einer vierten Dimension zu sein, das sowohl für Philosophen wie auch für Mathematiker und Physiker ein starker Beweis zum mindesten für die Möglichkeit einer vierten Dimension wurde und lange Zeit hindurch diese Rolle gespielt hat.

Heute ist jedoch auch diese Argumentation zugunsten einer vierten Dimension erschüttert, und zwar auf Grund einer schärferen Betrachtung jener geometrischen Verhältnisse. Es hat sich herausgestellt, daß der Widerspruch, den man in dem Verhalten solcher wie der angeführten geometrischen Gebilde sehen zu müssen glaubte, – um es kurz zu sagen – nur ein scheinbarer ist. Gehen wir zum Beweis des Gesagten zunächst nochmals auf die Dreiecke unserer Abbildungen 37 und 38 zurück. Die Dreiecke in Abbildung 38 sind im Schulsinne kongruent, das heißt sie stimmen in Seiten und Winkeln überein und lassen sich dennoch nicht durch Verschiebung innerhalb der Ebene zur Deckung bringen, wie es bei den kongruenten Dreiecken der Abbildung 37 ohne weiteres der Fall ist. Sind denn aber die Dreiecke der Abbildung 38 wirklich und vollkommen kongruent, das heißt: stimmen sie wirklich in allen räumlichen Beziehungen überein? Das ist nicht der Fall, denn Seiten und Winkel sind zwar in beiden Dreiecken gleich, aber sie sind in entgegengesetzter Richtung angeordnet. Die eingezeichneten Pfeilkreise lassen das deutlich erkennen. Bei dem linken Dreieck verlaufen Seiten und Winkel in der Richtung a, b, c, also von links nach rechts, in derselben Richtung wie ein Uhrzeiger, bei dem anderen Dreieck aber in der entgegengesetzten Richtung c, b, a, entgegen der Uhrzeigerrichtung. Die beiden Dreiecke unterscheiden sich also in einer sehr wesentlichen räumlichen Beziehung, durch die Anordnung ihrer Teile, oder durch den »Richtungssinn«, wie der Fachausdruck lautet. Sie sind also keineswegs völlig kongruent, und deswegen können sie auch nicht innerhalb der Ebene, durch bloße Verschiebung, zur Deckung gebracht werden, weil sie bei dieser Operation immer entgegengesetzten Richtungssinn beibehalten.

Entsprechendes wie hier von ebenen Figuren gilt auch von Körpern, also Gebilden dreier Dimensionen, die, wie rechte Hand und linke Hand, wie Original und Spiegelbild unsymmetrischer Körper überhaupt, selbst bei völliger Kongruenz von Seiten und Winkeln dennoch nicht zur Deckung gebracht werden können. Auch solche Körper sind nicht völlig kongruent, unterscheiden sich ebenfalls immer durch die entgegengesetzte Anordnung ihrer Teile, also den Richtungssinn. Sie ermangeln also in Wirklichkeit der völligen räumlichen Übereinstimmung, wodurch die Unmöglichkeit, solche Körper zur Deckung zu bringen, einwandfrei erklärt ist. Bei wirklich völliger Kongruenz, die also auch gleichen Richtungssinn einschließt, also bei Parallelstellung wie bei den Dreiecken in Abbildung 37, sind alle geometrischen Gebilde, gleichviel ob Flächen oder Körper, stets zur Deckung zu bringen, ohne daß es einer weiteren Dimension bedarf, um diese Operation auszuführen. Die Schuldefinition der Kongruenz hat lange Zeit das Moment des »Richtungssinnes« übersehen und damit der Spekulation eine Veranlassung zur Annahme einer vierten Dimension als Erklärungsweise gegeben. Die Aufdeckung des Richtungssinnes als Faktor der Kongruenz beseitigte den erwähnten Widerspruch und enthebt uns jeder Notwendigkeit, zur Erklärung der Erscheinungen, in denen man einen solchen Widerspruch sehen zu müssen glaubte, eine vierte Dimension anzunehmen. Abermals ist dieser Annahme ein Hauptargument entzogen.

Wir kommen also zu der vorläufigen Zusammenfassung: Ein unmittelbarer Beweis für das Vorhandensein einer vierten Dimension durch Erscheinen oder Verschwinden von Körpern ist noch niemals erbracht worden; das Argument für die Möglichkeit einer vierten Dimension, das bislang in der Unmöglichkeit gesehen wurde, bestimmte Körper, die im Schulsinne kongruent sind, zur Deckung zu bringen, ist entkräftet durch die einwandfreie andersartige Erklärung der Erscheinungen, von denen dieses Argument ausging.

Zugleich aber erhebt sich ein Argument von stärkster Beweiskraft gegen Vorhandensein oder Möglichkeit einer vierten Dimension, und dieses besteht in der vollkommenen Unmöglichkeit einer sinnfälligen Vorstellung einer vierten Dimension oder vierdimensionaler Gebilde. Nicht daß wir eine vierte Dimension nirgends finden oder wahrnehmen, wäre ein unbedingter Gegenbeweis gegen eine solche, denn wie bereits betont, sind wir von der Existenz vieler Dinge, wie der Atome, der Elektrizität usw., überzeugt, die wir nicht wahrnehmen und noch niemals wahrgenommen haben, aller Wahrscheinlichkeit nach auch niemals unmittelbar wahrnehmen werden; daß aber dem menschlichen Geiste überhaupt jede Möglichkeit fehlt, sich von vierdimensionalen Gebilden eine Vorstellung zu machen, darin sehe ich allerdings ein Argument von stärkster Beweiskraft gegen Vorhandensein und Möglichkeit einer vierten Dimension überhaupt. Die Atome, ihre Gestalt, Konstitution, Bewegung und Wirkungsweise, wie es die wissenschaftliche Theorie verlangt, können wir uns ohne Mühe vorstellen, eine Vorstellung, die bis zur Ausarbeitung konkreter Atommodelle gelangt ist; ebenso können wir uns von der Beschaffenheit und Wirkungsweise der Elektrizität eine sehr exakte Vorstellung machen, wie noch von zahllosen anderen Dingen, die es nach der Theorie gibt, ohne daß wir sie wahrnehmen können. Auf keine Weise aber ist einem Menschen eine sinnfällige Vorstellung einer vierten Dimension möglich, und damit verneint der menschliche Geist allen Theorien und Hypothesen zum Trotz in seinem Grunde selbst Möglichkeit und Vorhandensein einer vierten Dimension. Es müßten sich zum mindesten in unseren Vorstellungen und unserer Vorstellungsweise Andeutungen oder Übergänge finden lassen, die wir als Annäherungen an vierdimensionale Gebilde oder Vorgänge deuten könnten, aber nicht auch nur die geringsten Spuren solcher Art sind in unserem anschauenden und vorstellenden Bewußtsein zu finden. Die Psychologie des Menschen weist jede solche Möglichkeit ab. Für diese absolute Unmöglichkeit der sinnfälligen Vorstellung von Gebilden und Gestaltungen von mehr als drei Dimensionen aber kann ich keinen anderen Grund ausfindig machen als den, daß die Dreizahl der Dimensionen eine Naturkonstante ist, an die jedes menschliche oder sonstige Vorstellen auf diesem wie auf jedem anderen Planeten gebunden ist. Und wenn Fechner, wie bereits erwähnt, halb scherzhaft, halb ernst die Frage stellt, warum denn die Natur im Dimensionalen nur bis drei solle zählen können, so kann ihm darauf erwidert werden, daß noch in vielen anderen Beziehungen das Zählungsvermögen der Natur an ganz bestimmte Grenzen oder Konstanten gebunden ist. Es gibt nur fünf platonische Körper und kann nicht mehr als fünf geben; nur einmal sind in der unendlichen Zahlenreihe drei hintereinanderfolgende Primzahlen möglich, und die Zahl von 424 Meterkilogramm als Wärmeäquivalent ist nach unserer gesamten naturwissenschaftlichen Auffassung ebenfalls als eine Naturkonstante zu betrachten, die für das ganze Universum Geltung hat.

Damit erledigt sich auch die oft gebrauchte Analogie der zweidimensionalen Lebewesen, die sich zwar selbst keine sinnfällige Vorstellung einer dritten Dimension zu machen imstande sind, dennoch aber durch irgendwelche Erscheinungen auf das Vorhandensein einer solchen dritten Dimension schließen könnten, die ja, wie wir dreidimensionalen Menschen wissen, in Wirklichkeit vorhanden ist. Vielleicht wäre daher auch die menschliche Unfähigkeit, sich eine Vorstellung von der vierten Dimension zu machen, noch kein Beweis gegen die Möglichkeit oder das Vorhandensein einer solchen. Darauf ist zu erwidern, daß zweidimensionale Lebewesen nur eine Fiktion, nur eine begriffliche Erdichtung ohne Wirklichkeitswert sind, an die wir daher auch keinerlei Schlüsse für die Wirklichkeitswelt knüpfen können. Wir kennen Leben und Denken nur als Erscheinungen an selbständigen körperhaften, dreidimensionalen Wesen; Lebewesen zweier Dimensionen sind eine Unmöglichkeit, und daher kann auch das fiktive Denken und Vorstellen solcher fiktiven Wesen keinerlei Argumentation für die Wirklichkeitswelt ergeben, wenn wir jene zweidimensionalen Lebewesen auch zu Analogiezwecken verwenden.

Die Analogie mit den zweidimensionalen Lebewesen und ihrer zweidimensionalen Anschauungs- und Vorstellungsweise hat in den Untersuchungen und Theorien über die vierte Dimension eine große Rolle gespielt; Helmholtz hat diese Fiktion sehr ausgiebig für seine diesbezüglichen Untersuchungen benutzt, kam aber schließlich doch zu der Überzeugung, daß sich aus dieser Analogie keinerlei Schlüsse für die Möglichkeit oder Wirklichkeit einer vierten Dimension ziehen lassen, und ist daher bei dem dreidimensionalen Raume als Form der Wirklichkeitswelt geblieben.