Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

3. Der geheimnisvolle Würfel
(Das Delische Problem)

Ein Zauberkunststück – Die Forderung des Gottes – Das Rätsel der Würfelverdoppelung – Die Verdoppelung des Quadrates – Die Konstruktion der Quadratwurzel – Der nützliche »Pythagoras« – Die Konstruktion der Kubikwurzel – Ein fehlender Lehrsatz

Bei den Vorführungen vieler Zauberkünstler spielt oftmals ein geheimnisvoller Würfel eine große Rolle. Beispielsweise zaubert der Künstler aus einem solchen hohlen Würfel alle möglichen Dinge hervor, die weder ihrer Größe noch ihrer Zahl nach Platz in dem Würfel zu haben scheinen, oder er überdeckt mit einem solchen Würfel irgendeinen Gegenstand für einen Augenblick, und wenn er den Würfel dann wieder emporhebt, ist der Gegenstand verschwunden, oder es steht ein ganz anderes Ding auf dem Zaubertisch usw. Diese Kunststücke wirken immer sehr verblüffend; geht man der Sache jedoch auf den Grund, oder läßt man sich durch einen Fachmann die rätselhaften Vorgänge erklären, so wird der Würfel seines Geheimnisses freilich gründlich entkleidet, und es stellt sich heraus, daß das ganze Kunststück nur auf einer geschickten Täuschung der Zuschauer beruht. Dagegen gibt es ein anderes Geheimnis, das sich an den Würfel knüpft, dessen positive Lösung aber bis heute weder einem Zauberkünstler noch einem anderen Sterblichen gelungen ist, obwohl sich daran die scharfsinnigsten Forscher seit über zweitausend Jahren die Köpfe zerbrochen haben.

Welcher Art dieses merkwürdige Geheimnis des Würfels ist, darüber gibt schon eine Mitteilung aus dem Altertum Auskunft. Um das Jahr 400 v. Chr. wurde Griechenland von einer verheerenden Pest heimgesucht, die unheimlich lange anhielt, zahllose Opfer forderte und trotz aller Gebete und auch trotz aller ärztlichen Mittel nicht weichen wollte. Schließlich entschloß man sich, eine Abordnung nach dem berühmten Orakel des Gottes Apollo in Delos zu entsenden, die einen Spruch des Gottes erbitten sollte, was zu geschehen habe, um der Seuche Einhalt zu tun. Die Antwort, die der Gott durch den Mund der Pythia erteilte, lautete, die Pest würde zu Ende gehen, wenn man dem Gott einen Altar von dem doppelten Rauminhalt des im Tempel zu Delos stehenden Altars, der die Gestalt eines Würfels hatte, erbauen würde. Das schien sehr einfach, und bald war ein Altar von dem doppelten Rauminhalt des alten und von quaderförmiger Gestalt an Stelle jenes errichtet. Trotzdem aber wütete die Pest weiter, und als man das Orakel nochmals befragte, antwortete es, der neue Altar müsse nicht nur den doppelten Rauminhalt des alten haben, sondern auch wie dieser genau würfelförmig gestaltet sein. Auch das schien nicht schwer, und wiederum machte man sich schleunigst an die Arbeit, die Forderung des Gottes zu erfüllen, also einen Würfel von dem doppelten Rauminhalt des alten Altars zu erbauen. Da aber machte man die merkwürdige Erfahrung, daß die gestellte Aufgabe, die doch so leicht aussah, ganz ungeahnte Schwierigkeiten bereitete. Es gelang den Geometern, die zunächst beauftragt waren, die Längenverhältnisse bzw. die Seitenlänge des zu erbauenden Würfels zu bestimmen, nicht, mit den allein zur Verfügung stehenden geometrischen Hilfsmitteln, nämlich Zirkel und Lineal, die gesuchte Längengröße mit mathematischer Genauigkeit zu ermitteln. Deswegen wandte man sich schließlich an Plato, den berühmten Philosophen und Mathematiker, und bat um Rat, auf welche Art und Weise die gestellte geometrische Aufgabe zur Zufriedenheit des Gottes gelöst werden könnte. Wie sich die Sache mit der Pest weiter entwickelt hat, ist nicht berichtet; sie wird ja wohl einmal aufgehört haben, obwohl es nicht möglich war, der Forderung des Gottes nachzukommen. Denn auch Plato und seine Schüler, die sich mit Feuereifer an die Lösung der Aufgabe machten, waren nicht imstande, diese in völlig exakter, mathematisch absolut genauer Weise zu lösen. Auf keine Art und Weise war es möglich, mit Zirkel und Lineal, den bewährten Hilfsmitteln bei der Lösung aller geometrischen Aufgaben, die Seitenlänge eines Würfels, der den doppelten Rauminhalt eines gegebenen anderen Würfels haben soll, zu bestimmen. Man sah sich vor ein Rätsel gestellt, dessen Kernpunkt man trotz aller höchst scharfsinnigen Versuche und Untersuchungen nicht enthüllen konnte und das als Problem der Würfelverdoppelung oder als Delisches Problem in der Folgezeit, ähnlich wie die Quadratur des Kreises, eine der berühmtesten wissenschaftlichen Aufgaben wurde.

Wir wissen heute, welches der Grund der Unmöglichkeit ist, die verlangte Konstruktion nur mit Zirkel und Lineal auszuführen. Wir müssen, um diesen Grund zu erkennen, die Aufgabe zunächst algebraisch behandeln, das heißt, die geometrische Aufgabe in die Form einer Gleichung bringen. Diese Betrachtung erfordert nur ganz elementare mathematische Kenntnisse, deren sich jeder aus seiner Schulzeit erinnern wird, der dort überhaupt die Elemente der Geometrie und der Algebra kennengelernt hat.

Wir wollen, um den inneren Charakter der Aufgabe der Würfelverdoppelung zu erkennen, zunächst eine andere, ähnliche geometrische Aufgabe betrachten, nämlich die Verdoppelung eines Quadrates. Angenommen, wir haben ein Quadrat, dessen Seite die Länge a hat. Der Flächeninhalt dieses Quadrates ist dann a × a oder, in der üblichen Schreibweise, a ². Ein Quadrat von dem doppelten Flächeninhalt dieses Quadrates wäre dann 2a ² groß, und wir fragen: Wie können wir ein Quadrat von dem Flächeninhalt 2a ² mit Zirkel und Lineal konstruieren? Diese Aufgabe ist auf sehr einfache Art und Weise auszuführen. Um die Seitenlänge des gesuchten Quadrates zu bestimmen, müssen wir aus dem Ausdruck 2a ² die Wurzel ziehen. Bezeichnen wir die Seite des gesuchten Quadrates mit s, so erhalten wir mithin die Gleichung s = √2·a ² oder, wenn wir den Ausdruck unter dem Wurzelzeichen in eine angemessenere Form bringen, s = a√2.

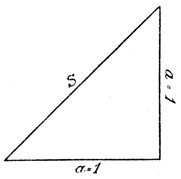
Abb. 5

Das ist also die algebraische Form, in die wir die ursprüngliche geometrische Aufgabe der Verdoppelung eines Quadrates gebracht haben, und die weitere Aufgabe besteht nunmehr nur noch darin, die Größe a√2 zu konstruieren. Das ist sehr einfach. Die Strecke a ist ja gegeben, es handelt sich also nur noch darum, den in jener Größe auftretenden Ausdruck √2, also die quadratische Wurzel aus 2, zu konstruieren. Auch das ist ohne Schwierigkeit möglich, denn wir sind in der Lage, jede Quadratwurzel zu konstruieren, und zwar mit Hilfe des pythagoreischen Lehrsatzes, der bekanntlich besagt, daß in jedem rechtwinkligen Dreieck die Summe der Quadrate über den beiden Katheten gleich ist dem Quadrat über der Hypotenuse. Um die Wurzel aus 2 zu konstruieren, brauchen wir nur einen rechten Winkel zu zeichnen, machen jeden Schenkel = 1 (etwa 1 Zentimeter oder eine sonstige Einheit lang) und verbinden die Spitzen der Schenkel. Dann entsteht das rechtwinklige und gleichseitige Dreieck unserer Figur 5, und bezeichnen wir in dieser die Hypotenuse mit s, so ist nach dem pythagoreischen Lehrsatz s ² = 1 ² + 1 ² oder s ² = 2, mithin s = √2. Die Hypotenuse in unserem Dreieck ist also die geometrische Konstruktion des algebraischen Ausdrucks √2. Ebenso könnten wir auch die Wurzel aus 3 konstruieren mit Hilfe eines neuen rechtwinkligen Dreiecks, dessen Katheten die Längen 1 und √2 haben. Die Hypotenuse des neuen Dreiecks wäre dann die geometrische Konstruktion der Wurzel aus 3. Damit ist die Lösung der Aufgabe selbst ohne weiteres gegeben. Haben wir ein Quadrat mit der Seitenlänge a und ziehen wir in diesem die Diagonale, die wir mit s bezeichnen wollen, so ist, wie wir auseinandergesetzt haben, nach dem Pythagoras s ² = 2a ², mithin s = a√2. Errichten wir nun über dieser Diagonale ein neues Quadrat, dessen Seitenlänge also a√2 ist, so ist der Flächeninhalt des ganzen neuen Quadrates gleich (a√2) ² = 2a ², also gerade doppelt so groß wie das Quadrat mit der Seitenlänge a, von dem wir ausgegangen sind. Um also ein Quadrat zu verdoppeln, brauchen wir nur über der Diagonale desselben ein neues Quadrat zu errichten, und da alle hierbei auftretenden Operationen mit Zirkel und Lineal ausgeführt werden können, so ist die Aufgabe der Verdoppelung eines gegebenen Quadrates damit einwandfrei gelöst.

Nunmehr wollen wir aus dem Gesagten die Nutzanwendung für unser eigentliches Problem, die Verdoppelung des Würfels, ziehen. Angenommen, wir haben einen Würfel von der Kantenlänge a, so ist der Rauminhalt dieses Würfels a × a × a oder in algebraischer Schreibweise, a ³. Ein Würfel von doppeltem Rauminhalt des gegebenen hätte mithin den Inhalt 2a ³, und um einen solchen Würfel zu konstruieren, müssen wir zunächst seine Kantenlänge bestimmen. Diese erhalten wir, wenn wir aus dem Ausdruck 2a ³ die dritte (oder kubische) Wurzel ziehen; bezeichnen wir die Kante des zu konstruierenden Würfels wieder mit s, so ist also s = ∛2a3, oder, in vereinfachter Form, a ∛2.

In diesem Ausdruck a ∛2, auf den uns die algebraische Behandlung unserer Aufgabe geführt hat, tritt also eine Wurzel vom dritten Grade oder eine kubische Wurzel auf, und wir fragen, ob und auf welche Weise wir diesen Ausdruck mit Zirkel und Lineal konstruieren können. Und da müssen wir leider sagen, daß dies auf keine Art möglich ist. Quadratische Wurzeln können wir, wie wir dargelegt haben, sehr leicht konstruieren, kubische Wurzeln aber nicht, und zwar deswegen nicht, weil uns für diesen Zweck nicht ein so bequemer Lehrsatz, wie es der pythagoreische Lehrsatz für die Konstruktion quadratischer Wurzeln ist, zur Verfügung steht. Für die Konstruktion kubischer Wurzeln gibt es einen solchen Lehrsatz nicht, und ein solcher kann auch niemals aufgestellt werden.

Das also ist der Grund, daß die Forderung des Gottes nicht erfüllt werden konnte und wir bis heute noch nicht in der Lage sind, die Aufgabe, die er stellte, mit Zirkel und Lineal allein mathematisch exakt zu lösen.

Selbstverständlich ist die Aufgabe nur in der beschriebenen exakten Form, also mit Zirkel und Lineal als alleinigen Hilfsmitteln, als nichtlösbar zu bezeichnen. In angenäherter Form und mit anderen Hilfsmitteln ist sie auf vielfache Weise, und zwar mit jeder gewünschten Genauigkeit, ausführbar, und in der Technik sind ja Aufgaben dieser Art sehr oft zu lösen. Auf diese technischen und Annäherungsmethoden hier einzugehen, bietet kein Interesse, dagegen werden wir bei dem Problem der Dreiteilung des Winkels sehr interessante und scharfsinnige Methoden dieser Art kennenlernen. Mit diesem Problem wollen wir uns in dem nächsten Aufsatz beschäftigen.