Der Wettlauf mit der Schildkröte

Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++

2. Die Quadratur des Kreises

Die Aufgabe – Quadratur und Rektifikation – Punkt und Linie – Die Monde des Hippokrates – Der Sinn der Platonischen Bedingung – Mittelalterliches – Technische Lösungen – Entdeckerfreuden und –leiden – Die Aufhellung des Geheimnisses – Die Zahl π – Quadratoren von heute

Das älteste und eigenartigste jener geometrischen Probleme, die sich an Zirkel und Lineal knüpfen, ist die Quadratur des Kreises. Es ist die berühmteste und, wenn man so sagen darf, zugleich auch die populärste jener geometrischen Aufgaben, und zwar deswegen, weil an der Lösung dieser Aufgabe die Jahrhunderte hindurch nicht nur die Mathematiker von Fach, sondern in ganz besonderem Maße auch die Laien ihren Scharfsinn erprobt haben. Diese sind es, die auch heute noch gerade an dieses Problem Zeit, Arbeit und Scharfsinn verwenden und dadurch die Aktualität dieser merkwürdigen geometrischen Aufgabe noch immer aufrechterhalten, während diese heute für die Wissenschaft selbst nur noch historische Bedeutung hat.

Rein äußerlich betrachtet, handelt es sich bei der Quadratur des Kreises um die anscheinend sehr einfache Aufgabe, zu einem gegebenen Kreise ein Quadrat zu zeichnen – oder vielmehr zu »konstruieren«, wie sich der Mathematiker ausdrückt –, das denselben Flächeninhalt wie der Kreis hat, wobei zur Konstruktion lediglich Zirkel und Lineal verwandt werden sollen. Aufgaben dieser Art, die man allgemein als »Verwandlungsaufgaben« bezeichnet, sind, sofern es sich nur um geradlinige Figuren handelt, sehr leicht zu lösen. So ist es beispielsweise spielend leicht, irgendein beliebiges Dreieck, Rechteck oder Vieleck in ein Quadrat zu verwandeln oder auch umgekehrt aus einem Quadrat oder Rechteck ein flächengleiches Dreieck zu machen, und im letztgenannten Falle sind sogar unendlich viele solcher Dreiecke möglich. Auch demjenigen, der nur über ganz elementare Kenntnisse in der Geometrie verfügt, sind solche Aufgaben und Konstruktionen geläufig, und daher ist es auch heute noch vielen unbegreiflich, daß das, was bei solchen wie den erwähnten Figuren so leicht und in so einfacher Weise ausgeführt werden kann, bei dem Kreise, diesem schönsten und regelmäßigsten unter allen geometrischen Gebilden, auf unüberwindliche Schwierigkeiten stoßen und daß diese Aufgabe sogar unlösbar sein soll.

Bemerkt sei noch, daß man unter Rektifikation des Kreises die Aufgabe versteht, die Umfangslinie oder Peripherie des Kreises in eine gerade Linie von gleicher Länge zu verwandeln, selbstverständlich ebenfalls nur vermittels Zirkel und Lineal. Beide Probleme stehen in engstem Zusammenhange, sind sogar im Grunde wesensgleich insofern, als mit der Lösung des einen zugleich auch die des anderen Problems gegeben wäre und die Unmöglichkeit der Lösung beider Probleme in derselben Wurzel zu suchen ist. Wir betrachten das Problem im folgenden lediglich von der Seite der Quadratur des Kreises aus.

Schon die Mathematiker des griechischen Altertums, bei denen die Geometrie zuerst ihre exakte Begründung erlangte, kannten das Problem und seine Tücken. Schon Pythagoras, dem der erste Beweis des nach ihm benannten Fundamentalsatzes gelang (um 500 v. Chr.), versuchte sich an der Lösung der Aufgabe, und der Geometer Hippokrates, der ein halbes Jahrhundert später in Athen lehrte, glaubte sogar die Lösung bereits gefunden zu haben, was sich dann aber, wie in so vielen derartigen Fällen, als Irrtum herausstellte. Die strenge präzis wissenschaftliche Formulierung und damit seine ganze Eigenart erhielt das Problem aber erst in der Philosophen- und Mathematikerschule Platos, der, wie für alle geometrischen Aufgaben, so auch für die Quadratur des Kreises die Bedingung aufstellte, daß diese nur mit Zirkel und Lineal ausgeführt werden dürfe. Erst durch diese Bedingung hat das Problem seine Schwierigkeit und seinen rätselhaften Inhalt erlangt. Wenn also der Mathematiker heute die Quadratur des Kreises als unlösbares Problem bezeichnet, so gilt das immer nur für die exakt mathematische Ausführung der verlangten Konstruktion, das heißt unter strikter Einhaltung der Platonischen Bedingung. Unter Zuhilfenahme noch anderer Hilfsmittel und ebenso für die annäherungsweise Ausführung, sogar für eine solche von jeder verlangten Genauigkeit, hingegen gibt es zahlreiche Methoden, und unter diesem Gesichtspunkt betrachtet ist die Quadratur des Kreises niemals ein Problem gewesen. Entsprechendes gilt auch von den erwähnten anderen geometrischen Aufgaben.

Machen wir uns zunächst die Eigenart unseres Problems unter dem Gesichtspunkte der Platonischen Bedingung allgemein klar. Die Konstruktion einer geometrischen Figur unter den genannten Bedingungen geschieht immer, indem man Linien zieht und auf diesen Punkte bestimmt, durch welche wiederum Länge und Richtung anderer Linien und dadurch schließlich die ganze gesuchte Figur bestimmt werden. Wenden wir das Gesagte auf unser Problem der Quadratur des Kreises an. In unserer Abbildung 1 haben wir einen Kreis dargestellt, dem ein Quadrat ABCD umgezeichnet und ein anderes Quadrat abcd eingezeichnet ist. Das umgeschriebene Quadrat hat, wie der Augenschein lehrt, einen größeren, das eingeschriebene Quadrat einen kleineren Flächeninhalt als der Kreis. Welches wäre nun das Quadrat, das denselben Flächeninhalt wie der Kreis hat? Es müßte seiner Größe nach augenscheinlich zwischen dem umgeschriebenen und dem eingeschriebenen Quadrat liegen, und seine vier Seiten müßten zwischen denen jener anderen beiden Quadrate verlaufen, etwa in der Weise wie die gestrichelten Linien in unserer Figur. Die vier Seitenlinien des gesuchten flächengleichen Quadrates müßten dann, wie aus der Zeichnung ohne weiteres hervorgeht, die vier Strecken Aa, Bb, Cc und Dd in je einem Punkte schneiden, und diese vier Punkte müßten dann die Eigenschaft haben, daß die durch sie gelegten vier geraden Linien ein dem vorgezeichneten Kreise flächengleiches Quadrat ergeben.

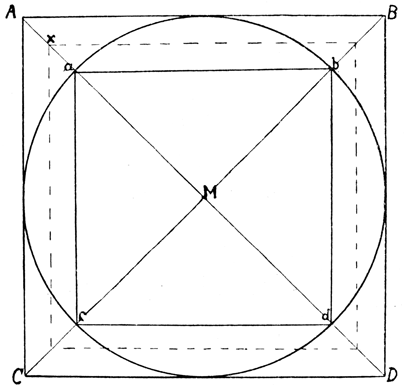
Abb. 1

Aber wie sind diese vier Punkte zu bestimmen, beispielsweise der Schnittpunkt x auf der Strecke Aa, auf der ja unendlich viele Punkte liegen? In der Abbildung 1 liegt der Punkt x etwa in der Mitte der Strecke Aa. Selbstverständlich ist aber keinesfalls gesagt, daß der Mittelpunkt dieser Strecke der gesuchte Punkt x wäre, und er ist das auch nicht. Ein Punkt in der Geometrie ist immer nur der Schnittpunkt zweier Linien, entweder zweier Geraden oder zweier Kreisbogen oder einer Geraden mit einem Kreisbogen. Das heißt also, um einen Punkt von bestimmten Eigenschaften zu finden, müssen sich aus den Voraussetzungen und Bedingungen der Aufgabe heraus zwei Linien bestimmen lassen, deren Schnittpunkt der Punkt mit den verlangten Eigenschaften ist. Für die Bestimmung des Punktes x ist uns aber leider nur eine gerade Linie gegeben, nämlich die Strecke MA, auf deren äußerem Abschnitt Aa der Punkt x liegen muß. Es gelingt nicht, aus den Voraussetzungen der Aufgabe heraus noch eine weitere gerade oder krumme Linie ausfindig zu machen, die durch den Schnittpunkt mit der Strecke Aa einen Punkt von der verlangten Eigenschaft bestimmt, und solange das nicht möglich ist, ist die Konstruktion des Quadrates, das dem vorgezeichneten Kreise flächengleich ist, mit Zirkel und Lineal unmöglich.

Diese Andeutungen mögen genügen, um den Charakter und die Eigenschaften geometrischer Probleme und Konstruktionen im allgemeinen und unseres hier behandelten Problems im besonderen anschaulich zu machen. Nur eins sei noch erwähnt, das spezielle Bedeutung für das Problem der Quadratur des Kreises hat: Man könnte die Frage aufwerfen, ob es zu einem gegebenen Kreise denn überhaupt ein Quadrat von genau, das heißt im mathematisch-exakten Sinne genau demselben Flächeninhalt gibt. Vielleicht gibt es ein solches überhaupt nicht, und vielleicht ist nur das der Grund der Unlösbarkeit der Aufgabe! Dem ist aber keinesfalls so, und die gestellte Frage ist unbedingt zu bejahen. Zwischen den beiden Quadraten ABCD und abcd in unserer Figur 1 gibt es eine unendliche Reihe von Quadraten, deren Flächeninhalt in stetiger, lückenloser Annäherung von dem Inhalt des kleineren zu dem des größeren aufsteigt, eins der dazwischenliegenden unendlich vielen Quadrate muß also auch von dem Flächeninhalte des gegebenen Kreises sein, dessen Flächeninhalt ja ebenfalls zwischen den Inhalten der bezeichneten beiden Quadrate liegt, denn sonst hätte jener Verlauf eine Lücke aufzuweisen. Das ist eine Folgerung, die durch die Stetigkeitstheorie der modernen Mathematik mit aller Sicherheit bestätigt wird. Also das gesuchte Quadrat, das dem gegebenen Kreise flächengleich sein soll, ist seiner Möglichkeit nach wirklich vorhanden, und die Aufgabe besteht nur darin, es unter den unendlich vielen Quadraten, zwischen denen es liegt, ausfindig zu machen und konstruktiv mit Zirkel und Lineal festzustellen.

Es gelang Plato und seinen Schülern nicht, das Problem unter der gestellten einschränkenden Bedingung zu lösen, und die Vergeblichkeit ihrer vielfachen und mit größtem Aufwand an Scharfsinn ausgeführten Versuche ließ die ganze Schwierigkeit und Tiefe des Problems in ihnen aufdämmern. Von der Lösbarkeit des Problems an und für sich war man überzeugt, und das um so mehr, als bereits damals bekannt war, daß sich in einem ganz bestimmten Falle der Flächeninhalt krummliniger – das heißt durch Kreisbogen begrenzter – Figuren auf den Flächeninhalt einer geradlinig begrenzten Figur zurückführen läßt. Diese Entdeckung rührt von dem bereits erwähnten griechischen Geometer Hippokrates her, der etwa ein Jahrhundert vor Plato in Athen wirkte, und die Figuren, um die es sich hierbei handelt, sind die nach ihrem Entdecker so benannten »Monde des Hippokrates«. Unsere Abbildung 2 veranschaulicht diesen Fall. Hier ist D ein rechtwinkliges Dreieck, über dessen Grundlinie ebenso wie über die beiden Seitenlinien der Halbkreis gezogen ist. Nach dem Verallgemeinerten pythagoreischen Lehrsatz ist der Flächeninhalt des Halbkreises A über der Grundlinie gleich der Summe der beiden Halbkreise B und C über den Seitenlinien, also A = C + B. Lege ich nun den Halbkreis A so, wie es Figur 3 zeigt, über die andere Seite der Grundlinie, so daß er durch die der Grundlinie gegenüberliegende Spitze des Dreieckes gehen muß, so überdeckt der Halbkreis A die beiden Halbkreise B und C zum Teil, so daß der Halbkreis C in die halbmondförmige Figur c und das Segment k, der Halbkreis B ebenso in den Halbmond b und das Segment p zerfällt. Es läßt sich nun leicht zeigen, daß die Summe der beiden Monde c und b gleich dem Dreieck D ist, denn der Halbkreis A ist nach dem Gesagten gleich der Summe b + p + c + k, das Dreieck D aber gleich dem Halbkreis A vermindert um p und k, also gleich b und c. Damit ist bewiesen, daß das Dreieck D den beiden Halbmonden c und b flächengleich ist. In schulmäßig-korrekter Form kommt das durch die folgenden Gleichungen heraus:
A = B + C D = A – p – k = B + C – p – k = B – p + C – k D = b + c

Das Dreieck D aber läßt sich wie jede geradlinige Figur dann mit Leichtigkeit in ein flächengleiches Quadrat verwandeln, und damit ist dann auch zugleich die Quadratur der beiden Monde, also zweier von Kreisbogen begrenzter Figuren, mit aller nur wünschenswerten mathematischen Exaktheit ausgeführt. Diese Monde des Hippokrates haben bei den Geometern des Altertums eine große Rolle gespielt. Hippokrates selbst glaubte durch seine Entdeckung die Quadratur des Kreises wenigstens im Prinzip möglich gemacht zu haben, und diese Auffassung wurde allgemein vorherrschend. War aber in einem Falle die Quadratur von durch Kreisbogen begrenzten Figuren gelungen, so mußte das, so folgerte man, auch bei dem Kreise selbst möglich sein, und so wurde die Entdeckung des Hippokrates ein Ansporn zu unermüdlicher Tätigkeit zur Lösung jenes Problems.

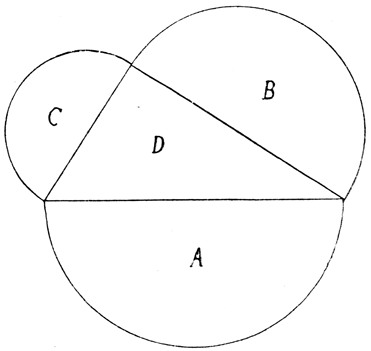
Abb. 2

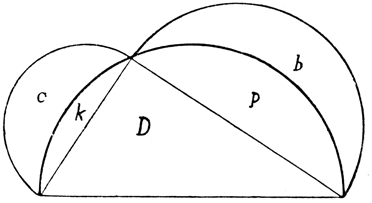
Abb. 3

Die an die Entdeckung des Hippokrates geknüpften Folgerungen stellten sich schließlich doch als Irrtum heraus; es zeigte sich, daß die Quadratur jener krummlinigen Figuren nur einen Spezialfall darstellt, der bindende Schlüsse für die allgemeine Aufgabe, alle krummlinigen Figuren überhaupt und insbesondere auch den Kreis in flächengleiche Quadrate zu verwandeln, nicht zuläßt, ein Fall, wie er in ähnlicher Weise in der Geschichte der mathematischen Probleme noch sehr oft auftritt. So blieb das Problem der Quadratur des Kreises trotz Hippokrates und trotz aller Versuche der Mathematiker des gesamten Altertums ungelöst, blieb es, was es war: ein vollkommenes Rätsel, dessen Kernpunkt man mit allem Scharfsinn nicht zu ergründen vermochte.

Vom Altertum übernahm das Mittelalter das Problem der Quadratur des Kreises als rätselhafte Erbschaft, die immer von neuem anspornte, die Lösung des Geheimnisses zu erforschen und wohl alle Mathematiker dieser Epoche mehr oder weniger beschäftigt hat. Warum sollte, was einst dem Hippokrates schon gelungen war, nämlich die Quadratur einer von Kreisbogen begrenzten Figur, nicht auch beim Kreise selbst gelingen? Die Geister, die Hippokrates und Plato beschworen hatten, wurden die Mathematiker des Mittelalters nicht los, und weil die Quadratur des Zirkels sich trotz aller Mühen und Methoden nicht finden lassen wollte und immer von neuem Rätsel aufgab, wurde das Problem in der noch sehr auf das Okkulte gerichteten Denk- und Auffassungsweise jener Zeit geradezu zu einer Art Mysterium von ganz derselben Bedeutung wie der Stein der Weisen, ein Geheimnis, hinter dem man den Grund der Dinge vermutete und dessen Lösung übermenschliche Gaben und Fähigkeiten verleihen sollte.

Weil die Lösung des Problems unter der einschränkenden Bedingung Platos nicht gelingen wollte, verlegten sich einzelne Mathematiker darauf, die Quadratur des Kreises wenigstens praktisch unter Zuhilfenahme anderer Hilfsmittel möglich zu machen. Verschiedene Methoden dieser Art wurden erfunden, darunter etliche höchst bemerkenswerte und scharfsinnige. Eine derselben rührt von Leonardo da Vinci, dem großen italienischen Maler, Bildhauer und Ingenieur, der zugleich auch ein vortrefflicher Mathematiker war, her und bestand in der Verwendung einer Walze. Ist nämlich ein Kreis gegeben, so wird eine Walze, deren Radius gleich dem des Kreises und deren Höhe gleich der Hälfte dieses Radius ist, einmal um ihren Umfang abgerollt, ein Rechteck beschreiben, das dem gegebenen Kreise genau flächengleich ist, wie jeder leicht nachprüfen kann, der über die Kenntnis der elementaren Kreisrechnung verfügt. Das Rechteck kann dann leicht in ein flächengleiches Quadrat verwandelt werden, und damit ist dann zugleich auch die Quadratur des ursprünglichen Kreises mit aller nur wünschenswerten Genauigkeit ausgeführt. Aber die hierbei verwandte Walze ist eben kein Hilfsmittel im Sinne der platonischen Bedingung, und solche Verfahren wie das von Leonardo da Vinci sind auch von den Mathematikern des Mittelalters niemals als wirkliche Lösung des Problems betrachtet worden.

Man hat oft die Frage aufgeworfen, ob die Bedingung, die Plato festlegte, nicht eine unnötige, zum mindesten gänzlich willkürliche, Erschwerung des Problems bedeute, und ob diese Bedingung mit dem mathematischen Charakter des Problems überhaupt etwas zu tun habe. Aber jene Bedingung hat ihren tiefen Sinn. Denn was bedeutet denn die Forderung, eine geometrische Konstruktion lediglich mit Zirkel und Lineal auszuführen? Sie bedeutet, daß die Lösung der gestellten Aufgabe eigentlich ohne alle äußeren Hilfsmittel, lediglich durch das Denken selbst, gefunden werden soll. Durch Überlegung werden die Punkte und Linien bestimmt, die die verlangte Konstruktion darstellen, und Zirkel und Lineal dienen dann lediglich als Hilfsmittel, um das durch das reine Denken Gefundene äußerlich zu fixieren. In dieser rein geistigen Methode sah und erkannte Plato das Wesen der Mathematik, und deswegen stellte er für die Lösung geometrischer Aufgaben jene Bedingung, die den Konstruierenden nötigt, die notwendigen Punkte und Linien erst durch reine Überlegung zu finden, ehe er sie graphisch fixieren darf. Indem die Mathematiker seit Plato jene Bedingung zum unverbrüchlichen Gesetz erhoben, haben sie den Charakter der Mathematik als einer reinen Vernunftwissenschaft festgehalten und durchgeführt. Jetzt ist ersichtlich, warum ein Verfahren wie das von Leonardo da Vinci keine Lösung des Problems im exakt wissenschaftlichen Sinne der Mathematik sein konnte; denn hierbei werden die nötigen Punkte und Linien, die die gesuchte Figur bestimmen, nicht durch das reine Denken ermittelt, sondern empirisch durch ein materielles Hilfsmittel, die Walze, gefunden und graphisch fixiert.

So ging der Kampf um das Problem bei Gelehrten und Laien weiter. Denn auch zahllose Laien, die mehr oder weniger mathematischer Bildung bar waren, beteiligten sich mit Feuereifer an der Ergründung des Geheimnisses. Warum sollte, was kein Verstand der Gelehrten sah, nicht in Einfalt das kindliche Gemüt eines Ungelehrten sehen und möglich machen? So kam es, daß die Quadratur des Kreises nicht nur das berühmteste und schwierigste, sondern zugleich auch eins der populärsten Probleme wurde, das mit Ehrfurcht erwähnt und erörtert wurde, wenn man auch sonst nichts weiter davon verstand, und in viele volkstümliche Schriften und Erzählungen, ja auch in Schwänke und Theaterstücke jener Zeit, spielte das Problem hinein. Sehr oft auch wurden erhebliche Geldpreise für die Lösung ausgesetzt, sowohl von wissenschaftlichen Instituten wie auch von für die Geometrie begeisterten Privatleuten, selbstverständlich für zahllose ein weiterer Anreiz, sich um die Lösung des hartnäckigen Rätsels zu bemühen, ohne daß aber jemals einer einen solchen goldenen Vogel abgeschossen hätte. Umgekehrt setzten aber auch oftmals Leute, die die Lösung des Problems gefunden zu haben glaubten, Belohnungen aus für den, der ihnen einen Fehler ihrer Lösung nachweisen könnte. So schrieb ein Franzose, Mathulon mit Namen, einen Preis von 1000 Talern aus für den Fall, daß jemand in seiner Quadratur des Kreises einen Fehler entdecken würde; ein zünftiger Mathematiker wies ihm einen Fehler nach, und Mathulon mußte bezahlen. Ein ähnliches Mißgeschick hatte auch ein polnischer Genieoffizier, der auf diese Weise um 50 Dukaten erleichtert wurde, und ähnliche Fälle gab es noch mehr. Auch durch den Beschluß der Pariser Akademie vom Jahre 1775, Prüfungen von angeblichen Quadraturen überhaupt nicht mehr vorzunehmen Siehe Seite 61., wurde die Problemfreudigkeit der Nichtzünftigen keineswegs gemindert. Die Volkstümlichkeit des Problems und die Bemühungen um seine Lösung erhielten sich nach wie vor.

Die wissenschaftliche Forschung selbst wurde durch die völlige Erfolglosigkeit aller die Jahrhunderte hindurch fortgesetzten Versuche um die Lösung des Problems, wie bereits dargelegt, schließlich zu der Auffassung geführt, daß eine exakte Lösung der Aufgabe überhaupt nicht zu erzielen sei. Damit begann eine neue Epoche in der Geschichte des Problems, die gekennzeichnet ist durch das Bemühen der Mathematiker, den exakten Beweis der Unmöglichkeit der verlangten Konstruktion unter der Platonischen Bedingung zu erbringen. Und auf diesem neuen Wege sollte sich endlich das Geheimnis des Problems dem forschenden Geiste erschließen. Nachdem Gauß schon nach Beginn des vorigen Jahrhunderts den Unmöglichkeitsbeweis für die verwandten Probleme der Dreiteilung des Winkels und des Delischen Problems erbracht hatte, war auch der Weg gewiesen, auf dem die Lösung des Problems der Quadratur des Kreises in diesem Sinne gesucht und gefunden werden mußte. Gauß hatte gezeigt, daß die erwähnten beiden Probleme unter der Bedingung Platos überhaupt nicht zu lösen sind, weil die Aufgaben in dieser einengenden Form auf algebraische Probleme führen, für die es eine Lösung nicht gibt und nicht geben kann, und die algebraische Behandlung der Aufgabe ließ gegen Ende des vorigen Jahrhunderts endlich auch das eigentliche Wesen der Quadratur des Kreises erkennen und ermöglichte es, auch für dieses schwierigste und am meisten umstrittene Problem den exakten Unmöglichkeitsbeweis zu erbringen. Wie bei jenen anderen beiden Problemen war es auch hier ein deutscher Mathematiker, dem dieser Beweis gelang. Im Jahre 1882 unterbreitete Ferdinand Lindemann, Professor der Mathematik in München, der wissenschaftlichen Welt den exakten Beweis der Unmöglichkeit der Quadratur des Kreises mit Zirkel und Lineal. Der Beweis beruht, um das Wesentlichste darüber zu sagen, auf der Eigenart der bekannten Zahl π, also 3,1415926 … usw., die das Verhältnis des Durchmessers eines Kreises zu seinem Umfange angibt. Diese Zahl ist, wie Lindemann nachwies, eine sogenannte transzendente Zahl. Eine solche Zahl hat neben ihren anderen merkwürdigen Eigenschaften auch die, sich nicht konstruieren zu lassen, das heißt, es können mit Zirkel und Lineal nicht zwei Strecken bestimmt werden, deren Längenverhältnis jener merkwürdigen Zahl entspricht, von denen also die eine soviel mal länger ist als die andere, wie der Umfang eines Kreises länger ist als sein Durchmesser Nach der genaueren Definition ist transzendent eine Zahl, die nicht Wurzel einer algebraischen Gleichung mit ganzzahligen Koeffizienten sein kann.. Die Zahl ist die Ursache der Unmöglichkeit der Quadratur des Kreises mit Zirkel und Lineal, sie hatte schuld, daß sich die Menschheit einige Jahrtausende hindurch den Kopf umsonst zerbrochen hat.

Mit dem exakten Beweis der Unmöglichkeit der Quadratur des Kreises im Sinne der Bedingung Platos hatte der Kampf um dieses hartnäckigste und schwierigste aller geometrischen Probleme, mit denen sich die Mathematiker jemals zu beschäftigen hatten, seinen Abschluß, das Problem selbst seine Lösung gefunden. Freilich war die Lösung anderer Art, als man einstmals gedacht hatte; sie war negativer Art und hatte die Alternative, ob die Lösung des Problems möglich oder unmöglich sei, mit dem exakten Beweis der Unmöglichkeit beantwortet, und für die Wissenschaft bedeutete das die vollkommene Entscheidung, an der nicht mehr zu drehen und zu deuteln ist. Der Kampf um das Problem war zu Ende gegangen, aber alles, was Gelehrte und Laien im Laufe vieler Jahrhunderte dazu beigetragen haben, wird für immer eins der eigenartigsten und reizvollsten Kapitel in der Geschichte des Forschens und des Strebens nach wissenschaftlicher Erkenntnis bleiben.

Postskriptum

Quadratoren von heute – Ein Arzt, ein Steinmetz und ein Orgelkünstler – Techniker als Quadratoren – Ein gelehrter Opponent – Die Quadratur des Kreises in der Fliederblüte

Wer über die Quadratur des Kreises schreibt und gemäß der wohlbegründeten Auffassung, zu der die Wissenschaft in dieser Frage gekommen ist, die Lösung dieses Problems als unmöglich bezeichnet, der muß mit Wehmut und Bedauern feststellen, daß die Mathematiker ihren Zeitgenossen unter allem, was da kreucht und fleucht, die vertrauensunwürdigsten Erzeugnisse der Schöpfung zu sein scheinen! Man glaubt ihnen einfach nicht, und ihre Behauptungen über das, was in der Mathematik als richtig und als falsch, als möglich und als unmöglich zu gelten habe, werden mit energischstem Widerspruch, mit mitleidsvollem Achselzucken oder auch mit Spott und Hohn und immer mit der strikten Behauptung, daß gerade das Gegenteil richtig sei, beantwortet. Diese Erfahrungen konnte ich nach einigen Veröffentlichungen über jenes Problem, insbesondere auch nach einem Rundfunkvortrag hierüber, überreichlich machen. Eine Unzahl von Zuschriften ging mir in diesem wie in jenem Falle zu, in denen mir haarscharf nachgewiesen wurde, daß alles, was ich über die Unmöglichkeit der Quadratur des Kreises gesagt und geschrieben hatte, nur eine Vorspiegelung kurioser Tatsachen oder eine Art fixer Idee von mir sei. Und gleichzeitig wurden mir die verschiedenartigsten geometrischen Konstruktionen übersandt, die die absolute Lösung dieses Problems enthalten sollten. Das sind die Quadratoren von heute, die modernen Vertreter jener niemals ausgestorbenen und niemals aussterbenden, nicht unsympathischen Gattung, die auf eigene Faust die Lösung jenes Problems, das der Wissenschaft selbst unüberwindliche Schwierigkeiten bereitete, erzwingen will.

Lassen wir Beispiele sprechen: Ein Dr. med. schrieb mir, er sei jederzeit in der Lage, sowohl die Dreiteilung des Winkels wie auch die Quadratur des Kreises in exakter Weise nur mit Zirkel und Lineal auszuführen. Die Gründe, die die Mathematiker für die angebliche Unmöglichkeit dieser Konstruktion anführten, seien nichts weiter als Verlegenheitsphrasen, um die eigene Unfähigkeit zu verdecken. Er fechte grundsätzlich jede dieser Behauptungen, wo immer er sie finde, an und fordere alle Mathematiker der Welt heraus, seine Beweise nachzuprüfen, aber noch keiner habe den Mut gehabt, seine Forderung anzunehmen! Wie gesagt, das schrieb ein Arzt. Nun sind ja unzweifelhaft Medizin und Mathematik nicht unwesentlich verschiedene Gebiete des Wissens und Könnens, aber darin sollten sie sich doch ähneln, daß die Leidenden hier wie dort dem Fachmann wenigstens das notdürftigste Vertrauen entgegenbringen müssen. Der Herr hat mich dann auch einmal aufgesucht, ein liebenswürdiger älterer, temperamentvoller Herr; sein Geheimnis hat er mir nicht enthüllt, und das Vertrauen, dessen ich zu seiner »Heilung«, das heißt zum Nachweis der Irrigkeit seiner Annahmen und Behauptungen bedurfte, konnte er nicht aufbringen. Er glaubte mir eben nicht.

Ein anderer Fall: Ein wackerer Steinmetzmeister schrieb mir, er begreife absolut nicht, wie man zu der Behauptung komme, daß die Quadratur des Kreises unmöglich sei; er komme durch seinen Beruf täglich in die Lage, diese ausführen zu müssen, und wolle mir gern Unterricht erteilen. Darauf folgte noch die zarte Mahnung, die Rückerstattung des seinerzeit für mich angewandten Schulgeldes zu beantragen, und nachdem der Gute so seine Verachtung aller Wissenschaft noch mit dem üblichen »Hochachtungsvoll« bekräftigt hatte, gab er in einem Postskriptum seinen Gefühlen noch mit den mannhaften Worten Ausdruck: »Die Gelehrten sind eben allens Ochsen!« Ein anderer meiner Leser sandte mir seine Konstruktion zur Quadratur des Kreises ein; ich sandte sie ihm mit dem Hinweis auf die sehr kindlichen Fehler zurück. Schon wenige Tage darauf bekam ich von ihm eine Neubearbeitung mit der Versicherung, daß die begangenen Fehler ausgemerzt seien und diesmal die Lösung unwiderruflich richtig sei. Auch diese Ausarbeitung ging mit den angestrichenen Fehlern an ihren Urheber zurück mit dem Erfolg, daß nach einer knappen Woche eine abermalige Bearbeitung des Unermüdlichen ankam. Nach der sechsten Bearbeitung gab ich das Rennen auf, und seitdem mag mein Kredit als Wissenschaftler bei diesem Forscher von eigenen Gnaden auf dem absoluten Nullpunkt angelangt sein. Aus einer Kleinstadt im Osten unseres Vaterlandes aber kam mir ein Brieflein zu, zwar von zarter Hand, aber voll mannhaften Tones und des Inhaltes, daß die Absenderin meine Veröffentlichung zur Veranlassung nehmen werde, um im Kreisblatt einen Artikel »über den unglaublichen Aberglauben« zu schreiben, der anscheinend noch bei vielen sogenannten Intellektuellen grassiere; denn mit der Quadratur des Kreises habe man sich wohl in früheren dunklen Zeiten beschäftigt und sie damals für unmöglich erklärt, aber heute wisse jeder aufgeklärte Mensch, daß das eben nur ein Aberglauben sei. Ob der vernichtende Leitartikel im Kreisblatt erschienen ist, weiß ich nicht, aber ich habe lange in zitternder Erwartung geschwebt. Ein anderer dieser privaten Forscher, ein wackerer Orgelbauer, aber veröffentlichte in der Fachzeitung seines Gewerbes eine Entgegnung, in der er an einer ebenso kunstvollen wie fehlerhaften Zeichnung bewies, daß es ihm gelungen sei, die Quadratur des Kreises zu finden, und die Redaktion des betreffenden Blattes, die von der Sache wohl geradesoviel verstand wie der geschätzte Mitarbeiter, begleitete dessen Abhandlung mit hoheitsvollen Worten über die Unzulänglichkeit der offiziellen Wissenschaft im allgemeinen und die der Mathematiker im besonderen, die sich hier von einem einfachen, ungelehrten und unstudierten Werkstattechniker beschämen lassen müßten. Ich habe mich lange sehr bedrückt gefühlt!

Man irrt aber, wenn man annimmt, daß die Unmöglichkeit der Quadratur des Kreises oder der Lösung der verwandten geometrischen Probleme etwa nur von Leuten bestritten werde, die es bisher verschmähten, mit der Mathematik nähere Bekanntschaft zu machen. Eine ganze Anzahl solcher wie oben gekennzeichneter Schreiben ging mir auch von Technikern, Diplom- und anderen Ingenieuren zu, also von Leuten, die doch von Berufs wegen mit einem tüchtigen Teil mathematischer Kenntnisse ausgerüstet sind. Sie alle sandten mir auch technische Zeichnungen und umfangreiche Beweise, die die Richtigkeit ihrer Auffassung dartun sollten, und ich gebe gern zu, daß die Beweiskonstruktionen von dieser Seite im allgemeinen schwieriger und interessanter waren als die vieler anderer Quadratoren, die sich die Sache manchmal doch allzu leicht machen. Besonders mit interessanten Kurvenkonstruktionen suchen die Herren von der technischen Fakultät dem Problem gern zu Leibe zu gehen, aber da alle Kurven außer dem Kreise andere Hilfsmittel als Zirkel und Lineal erfordern, so konnte auch niemals einer dieser Versuchskonstruktionen der Preis der Anerkennung zuerteilt werden. Sogar ein Dozent einer Technischen Hochschule war unter den Quadratoren, die meine Veröffentlichung zum Widerspruch, sogar zu einem äußerst geharnischten, herausgefordert hatte. Dieser Opponent schrieb an die Redaktion des Blattes, in dem meine Veröffentlichung erschienen war, einen flammenden Protest, meinte, daß der Verfasser dieser Abhandlung anscheinend nicht über die Kenntnisse eines Obertertianers verfüge, und fügte Zeichnung und Berechnung bei, wie sowohl die Quadratur des Kreises wie die Dreiteilung des Winkels auszuführen sei, Ideen, die bei einem Lehrer einer Technischen Hochschule, der, wenn er auch nicht eigentlicher Mathematiker ist, so doch einem technischen Fachgebiete angehört, als in hohem Maße bemerkenswert anmuten mußten. Der unbekümmerte Ton seines Schreibens führte dann zu einer sehr deutlichen Auseinandersetzung, in deren Verlauf sich mein rabiater Ankläger genötigt sah, der Redaktion des Blattes wie auch mir gegenüber seine merkwürdigen Behauptungen selbst als Irrtum zu bezeichnen, den kränkenden »Obertertianer« reuevoll zurückzunehmen und schließlich noch einen Barbetrag für bereits entstandene gerichtliche Kosten zu bezahlen. Die Person des Beteiligten hat diesen Fall immerhin bemerkenswert gemacht.

Daß der mathematisch gebildete Techniker die von ihm ersonnene Annäherungskonstruktion gern für die vollendete Lösung des Problems zu halten geneigt ist, hat seinen tieferen psychologischen Grund. Der Techniker, der Mann der Praxis, neigt sehr begreiflicherweise dazu, das, was sich mit technischen Hilfsmitteln und Methoden erreichen läßt, auch bei einem mathematischen Problem für die exakte Lösung zu halten, besonders dann, wenn die Konstruktion augenscheinlich einen hohen Genauigkeitsgrad aufzuweisen hat. Aber die Mathematik sieht ihre Probleme mit anderen Augen an. Sie hat mit den Hilfsmitteln und Methoden der Technik nichts zu tun, auch nicht bei der Lösung der mathematischen Probleme, und was dort als richtig und zulässig gilt, ist das noch keineswegs im Gebiet der sogenannten reinen Mathematik, die alle äußeren oder auf der bloßen Erfahrung beruhenden Methoden und Hilfsmittel abweist und durch reines Denken zu ihren Ergebnissen und Beweisen gelangen will. An dieser Unterscheidung gehen selbst viele mathematisch Gebildete vorbei, und daraus ergibt sich dann die heftige Anfeindung der Auffassung der wissenschaftlichen Mathematik gerade seitens dieser Kreise.

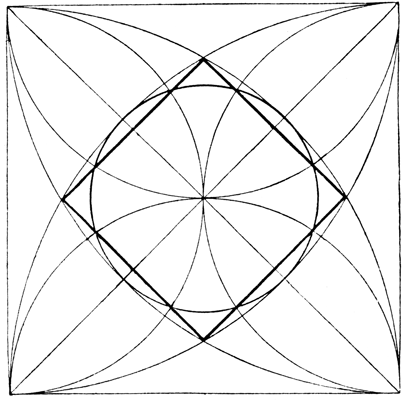
Abb. 4
Die Quadratur des Kreises in der Fliederblüte

Eine sehr interessante, wenn natürlich ebenfalls nicht exakte Versuchskonstruktion zur Quadratur des Kreises sei noch erwähnt. Sie stammt von Oberleutnant K., der sie mir zur Prüfung unterbreitete. Er hatte, wie er mir erzählte, als er im Felde war, in Mußestunden Gelegenheit gehabt, die Blüte des Flieders zu studieren, und an dieser war ihm das exakte mathematische Verhältnis aufgefallen, das ihm die Lösung des Problems der Quadratur des Kreises zu sein schien. Die nebenstehende Abbildung zeigt das geometrische Bild der Fliederblüte. Die Konstruktion ist aus der Abbildung ohne weiteres ersichtlich. Verbindet man die vier Punkte, in denen sich die Viertelkreise schneiden, so erhält man ein Quadrat; schlägt man dann um den Mittelpunkt dieses Quadrates einen Kreis, der die Viertelkreise berührt, so sind, wie Herr K. annahm, dieser Kreis und das Quadrat flächengleich. Tatsächlich glaubte er, in dem mathematischen Bild der Fliederblüte die Lösung des uralten Problems der Quadratur des Kreises sehen zu dürfen, von der Erwägung ausgehend, daß die Natur sicherlich doch zustande bringen könne, was dem Scharfsinn der Mathematiker bislang entgangen sei. Die Prüfung ergab dann freilich, daß auch dieses mathematische Naturbild nicht als vollkommene Quadratur bezeichnet werden kann, denn Quadrat und Kreis sind nicht vollkommen flächengleich, wie die analytische Berechnung ihrer Flächeninhalte ohne weiteres ergibt. Wohl aber ist die Verschiedenheit der beiden Flächeninhalte nur eine verhältnismäßig geringe; sie beträgt nur etwa ein Hundertstel des Kreisinhaltes, so daß das Bild der Fliederblüte immerhin als eine ziemlich genaue und auf alle Fälle überaus interessante Annäherungskonstruktion bezeichnet werden darf. Aber selbst wenn die Rechnung absolute Übereinstimmung der beiden Flächeninhalte ergeben hätte, wäre das doch keine exakte Quadratur gewesen, denn bei einer solchen dürfen nur Zirkel und Lineal als Hilfsmittel verwandt werden. Die Natur, die ihre Gebilde auf ihre Weise schafft, hätte also, selbst wenn sie die Quadratur rechnerisch mit absoluter Genauigkeit irgendwo herstellte, sich dabei unzulässiger Hilfsmittel bedient, und das darf auch die Natur nicht, wenn sie den Anforderungen der exakten Mathematiker genügen will!