Der Wettlauf mit der Schildkröte

Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++

5. Das Problem der Kreisteilung

Noch ein Kreisgeheimnis – Vom 3- und 6-Eck, vom 5-, 10- und 15-Eck – Der Drudenfuß – Die heilige Sieben – Ein altes Problem und ein junger Student – Die Entdeckung der 17-Teilung des Kreises – Die Gaußschen Kreisteilungszahlen – Ohne Lineal

In der Quadratur des Kreises haben wir das bekannteste und berühmteste Problem kennengelernt, das sich an die Kreisfigur knüpft. Aber die Quadratur ist keineswegs das einzige Geheimnis des Kreises. Ein anderes und kaum weniger reizvolles Problem dieser Art ist auch die Kreisteilung, das heißt die Aufgabe, die Kreislinie, gelehrt als Peripherie bezeichnet, mit Zirkel und Lineal in eine Anzahl gleicher Teile zu teilen. Dieses Problem ist in Laienkreisen viel weniger bekannt als das der Quadratur, obwohl sich auch an diese Aufgabe eine lange und inhaltreiche Geschichte und eine Fülle überaus interessanter Konstruktionen und Einzelfragen knüpft.

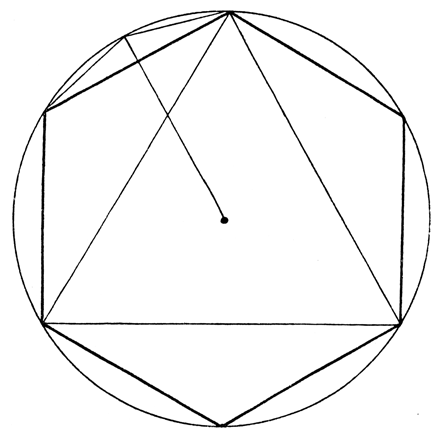
Abb. 15
Die 3-, 6- und 12-Teilung des Kreises

Sehr viele Fälle der Kreisteilung sind leicht und einfach auszuführen, und solche Fälle werden bereits in der Schulgeometrie gelehrt. Das Problematische dieser Konstruktionen steckt vielmehr in bestimmten Einzelfällen, für die es unter der Platonischen Bedingung keine Lösung gibt. Betrachten wir zunächst kurz die möglichen Fälle der Kreisteilung. Um beispielsweise einen Kreis in zwei Teile zu teilen, braucht man nur durch den Mittelpunkt des Kreises eine gerade Linie zu ziehen, deren Schnittpunkte mit der Peripherie diese in zwei gleiche Teile teilen. Errichtet man dann auf diesem Durchmesser im Mittelpunkte nach beiden Seiten eine lotrechte Linie, so wird hierdurch der Kreis in vier gleiche Teile geteilt, und verbindet man die erhaltenen vier Teilungspunkte durch gerade Linien, so erhält man ein regelmäßiges Viereck oder Quadrat. Auch die Sechsteilung ist überaus einfach und geschieht, indem man den Radius oder Halbmesser des Kreises von irgendeinem Punkte der Kreislinie an hintereinander auf dieser abträgt; das sechste Teilstück hört dann dort auf, wo das erste anfing, und damit ist die Konstruktion ausgeführt. Durch Verbindung dieser Teilungspunkte erhält man das regelmäßige Sechseck, bei dem also alle Seiten und Winkel gleich groß sind, eine sehr schöne geometrische Figur, die in der Mythologie, in Sitte und Glauben, allerdings auch im Aberglauben vieler Völker eine große Rolle gespielt hat. Die Entdeckung der Sechsteilung des Kreises und die Konstruktion des regelmäßigen Sechseckes in dieser Weise soll bereits den alten Babyloniern gelungen sein. Selbstverständlich kann in leichter Weise der Beweis geführt werden, daß durch diese Operation die Kreislinie auch wirklich mit mathematischer Exaktheit in sechs Teile geteilt wird. Verbindet man je zwei der sechs Teilungspunkte, indem man immer einen Punkt übergeht, so teilen die übrigen drei Punkte die Kreislinie in drei gleiche Teile, und man erhält das regelmäßige oder gleichseitige Dreieck, wie es unsere Abbildung 15 veranschaulicht. Ferner können wir, wenn eine bestimmte Teilung gelungen ist, leicht und einfach eine Teilung der Kreislinie von der doppelten Teilungszahl bewirken. Wenn wir beispielsweise in unserer Figur 15 die Seite des regelmäßigen Sechseckes, das die stark gezeichneten Linien darstellen, halbieren und durch diesen Halbierungspunkt eine gerade Linie vom Mittelpunkte des Kreises bis zur Peripherie legen, so ist hierdurch das Bogenstück über der Seite des Sechseckes ebenfalls in zwei Teile geteilt, und führen wir diese Operation bei allen sechs Seiten aus, so ist hierdurch der Kreis in zwölf gleiche Teile geteilt, und durch Verbindung dieser Teilungspunkte ergibt sich das regelmäßige Zwölfeck. Auf entsprechende Weise können wir dann auch die 24-, die 48-, die 96- usw. Teilung des Kreises ausführen, ebenso aus der 2- oder 4-Teilung auch zu der 8-, der 16-, der 32-, der 64- usw. Teilung gelangen und die entsprechenden regelmäßigen Vielecke konstruieren, alles Operationen, bei denen wir lediglich Zirkel und Lineal benötigen. Auf diese Weise erhalten wir also bereits eine überaus große Anzahl von Kreisteilungen.

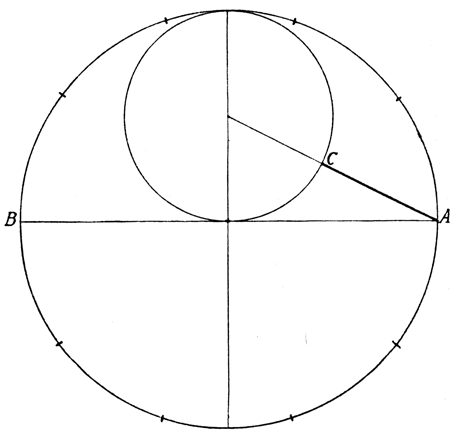
Abb. 16.
Die 10-Teilung des Kreises

Etwas verwickelter, aber auch noch sehr einfach ist die 10-Teilung des Kreises. Sie wird in mathematischer Weise ausgeführt, indem man, wie es unsere Abbildung 16 zeigt, durch den Mittelpunkt des gegebenen Kreises zunächst zwei aufeinander senkrechte Durchmesser legt, dann um den Mittelpunkt eines der so erhaltenen Halbmesser einen Kreis schlägt und den Mittelpunkt dieses kleinen Kreises mit dem Punkte A verbindet, in welchem die zu teilende Kreislinie sich mit dem anderen Durchmesser schneidet. Diese Verbindungslinie schneidet den kleinen Kreis in dem Punkte C, und trägt man die so erhaltene Strecke AC von irgendeinem Punkte der Kreislinie, also etwa von A an, auf dieser ab, so wird die Kreislinie hierdurch in zehn gleiche Teile geteilt. Durch Verbindung dieser Teilpunkte erhalten wir dann das regelmäßige Zehneck. Durch Überspringen je eines Teilpunktes gelangt man dann auch zur Fünfteilung und durch Verbindung dieser Teilungspunkte zur Konstruktion des regelmäßigen Fünfeckes.

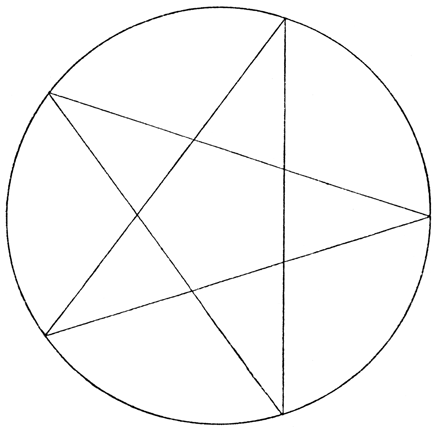
Abb. 17
Der Drudenfuß

Ein anderes Fünfeck zeigt unsere Abbildung 17. Es entsteht, indem man bei der Verbindung der Teilpunkte immer einen Punkt überspringt; der letzte Verbindungszug kehrt dann zum Ausgangspunkt zurück; das Mittelstück dieser ebenfalls sehr interessanten Figur zeigt dann wieder ein kleines regelmäßiges Fünfeck. Diese Figur, Pentagramm oder – volkstümlicher – Drudenfuß genannt, nimmt im Glauben und Aberglauben einen noch größeren Raum als das bereits erwähnte Sechseck ein. Diese Figur sollte, auf der Schwelle ausgezeichnet, Teufel, Hexen und böse Geister vom Hause fernhalten. »Das Pentagramma macht dir Pein?« fragt in diesem Sinne Faust spöttisch Mephisto, der sich in einer solchen Figur gefangen hat und nun nicht wieder heraus kann.

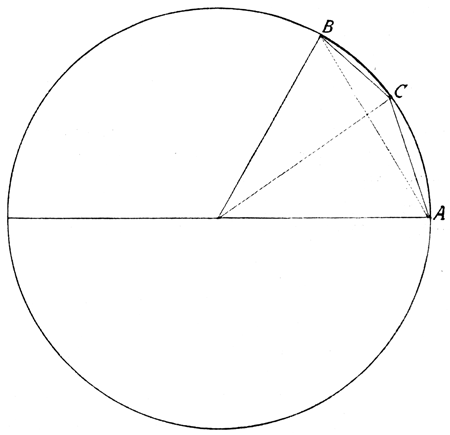
Abb. 18
Die 15-Teilung des Kreises

Von der Zehnteilung gelangen wir durch Halbierung dann auch zur 20-, 40-, 80- usw. Teilung des Kreises und zur Konstruktion der entsprechenden Vielecke. Endlich können wir in dieser Weise, also nur mit Zirkel und Lineal, auch noch die 15-Teilung ausführen. Sie geschieht, indem man von irgendeinem Punkte A der Peripherie erst den sechsten Teil, der dem Bogen AB entspricht (Abb. 18), dann von demselben Punkte aus den zehnten Teil des Kreisumfanges (Bogen AC) abträgt. Die Differenz zwischen diesen beiden Bogenstücken, in unserer Figur also der Bogen BC, ist der fünfzehnte Teil des Gesamtumfanges des Kreises, denn es ist ¹/ ₆ – ¹/ ₁₀ = ¹/ ₁₅. Durch Halbierung gelangen wir dann auch zur 30-, 60-, 120- usw. Teilung und den entsprechenden regulären Vielecken.

Damit sind aber auch die Möglichkeiten der Kreisteilung in der geschilderten elementaren Weise erschöpft. Zwar können auf diese Weise zahlreiche Teilungen ausgeführt, noch viel mehr aber nicht ausgeführt werden. Beispielsweise fehlen unter den angegebenen Teilungen die 7-, 9-, 11-, 13- usw. Teilung und ebenso, um auch einige höhere Teilungszahlen zu nennen, die 35-, 70-, 86-, 87-, 88-, 90- usw. Teilung, und ebenso auch die entsprechenden regelmäßigen Vielecke. Diese Teilungen und Konstruktionen also konnten mit Zirkel und Lineal nicht bewirkt werden, soviel man auch forschte und so viele verschiedenartige Methoden man für diesen Zweck auch ersann. Sind die 2-, 3- und 5-Teilung und die hieraus durch Halbierung und Kombination abgeleiteten Teilungen und Konstruktionen die einzigen oder sind noch andere möglich? Das war die Frage, die sich den Mathematikern aufdrängte und die Antwort von ihnen heischte.

Auch dieses Problem hat schon die ältesten Geometer beschäftigt, ja in seiner einfachsten Form ist es sogar älter als die Quadratur des Kreises. Denn Kreisteilungen und Vieleckskonstruktionen waren von jeher für die verschiedensten praktischen, technischen und wissenschaftlichen, besonders auch astronomischen Zwecke notwendig, und das führte naturgemäß schon in frühester Zeit zu Versuchen und Methoden, auch alle übrigen Kreisteilungen auszuführen. Schon Ägypter und Babylonier suchten diese Probleme zu lösen, angeregt vor allem durch die Beschäftigung mit der Astronomie, die besonders bei den Babyloniern bereits in hoher Blüte stand, und von diesen Völkern ging die Beschäftigung mit den Problemen der Kreisteilung dann auch auf die Griechen über, bei denen diese, wie die gesamte Geometrie überhaupt, ihre präzis wissenschaftliche Formulierung erhielten, vor allem durch die Bedingung Platos, die auch für die Lösung dieser Probleme und die Ausführung der entsprechenden Konstruktionen Zirkel und Lineal als einzig zulässige Hilfsmittel festsetzte. Unter diesen einengenden Bedingungen aber gelang die Ausführung weiterer Teilungsarten als der genannten nicht, soviel Scharfsinn und Arbeit die Geometer seit Pythagoras' Zeiten auch diesen Problemen zuwandten. Insbesondere auf die Siebenteilung des Kreises wurde die Jahrhunderte hindurch sehr viel Arbeit und Scharfsinn verwandt, denn die Sieben galt von jeher als heilige Zahl, und daher war die Siebenteilung des Kreises und die Konstruktion des regelmäßigen Siebenecks mit Zirkel und Lineal ein besonders eifrig verfolgtes Ziel der Geometer. In den engeren Kreisen der Mathematiker spielte die Siebenteilung kaum eine geringere Rolle als die Quadratur des Kreises.

Auch hier ging es wie bei den anderen großen Problemen, die sich an Zirkel und Lineal knüpfen. Die Mathematiker des Altertums wie des Mittelalters versuchten sich ebenso eifrig wie vergeblich auch an diesem Problem, und zahlreiche Methoden wurden erdacht, die aber alle nicht zum befriedigenden Ziele führten. Bei alledem müssen wir uns auch hier vor Augen halten, daß die verlangten Teilungen und Konstruktionen eben nur unter der einschränkenden Platonischen Bedingung, also nur, wenn Zirkel und Lineal als einzige Hilfsmittel zur Verfügung kommen sollen, unmöglich sind. Bei Verwendung anderer Hilfsmittel sind ausnahmslos alle Teilungsarten und die Konstruktion aller regelmäßigen Vielecke, wenn auch nur in angenäherter Form, möglich. Die erreichbare Annäherung reicht für alle überhaupt in Betracht kommenden Zwecke in Technik und Wissenschaft vollkommen aus und kann bis zu jedem beliebigen Genauigkeitsgrade geführt werden. Schon die ältesten Kulturvölker haben uns zahlreiche Darstellungen von Vielecken hinterlassen. Das regelmäßige Siebeneck kommt in diesen Darstellungen sehr oft vor, und die Wagenbauer der ältesten Zeit verstanden sich schon darauf, Wagenräder mit sieben Speichen zu konstruieren, müssen also schon Annäherungsmethoden von ausreichender Genauigkeit gekannt haben.

Für die Wissenschaft der Mathematik freilich waren solche Annäherungsmethoden, selbst die genauesten, keine Lösung des Problems. Für diese bestand eben das Problem darin, die verlangte Teilung und Konstruktion lediglich mit Zirkel und Lineal auszuführen, und unter dieser Bedingung spottete das Problem allen Lösungsversuchen. Wie bei der Quadratur des Kreises, beim Delischen und beim Winkelteilungsproblem, sah man sich auch hier vor ein Geheimnis gestellt, das unergründlich schien. Und weil dem so war und alle Lösungsversuche immer wieder mit Mißerfolgen endeten, neigten viele Gelehrte der Ansicht zu, daß weitere als die obenerwähnten Kreisteilungen, die sich aus den Grundteilungszahlen 2, 3 und 5 ergeben, überhaupt unmöglich seien, ohne allerdings den Beweis für diese Ansicht, der also ein Unmöglichkeitsbeweis gewesen wäre, erbringen zu können, und diese Sachlage blieb bis gegen Ende des 18. Jahrhunderts unverändert bestehen.

Daher mußte es gewaltiges Aufsehen nicht nur bei den Mathematikern, sondern in der gesamten wissenschaftlichen Welt überhaupt erwecken, als im Jahre 1796 ein blutjunger Student bewies, daß die Reihe der Kreisteilungen mit den erwähnten Arten doch noch nicht abgeschlossen und beispielsweise auch die 17-Teilung des Kreises und dementsprechend auch die Konstruktion des regelmäßigen 17-Ecks mit Zirkel und Lineal möglich ist. Dieses jugendliche Genie, das mit dieser Tat die über zweitausend Jahre alte Lehre von der Kreisteilung mit einem Schlage zu neuem Leben und neuer Entwicklung brachte, war der damals neunzehnjährige Karl Friedrich Gauß. Die krumme Zahl 17, an die man in der Geschichte der Kreisteilung wohl nur höchst selten gedacht haben mag, gelangte plötzlich zu ungeahnter Bedeutung und wurde eingereiht unter jene auserwählten Zahlen, für die die Kreisteilung in mathematisch exakter Weise möglich ist. Die Mathematiker standen Kopf, und mit ihnen noch viele andere Leute. Ja, wenn es wenigstens noch die heilige 7 gewesen wäre, aber ausgerechnet 17!

Doch es blieb bei der krummen 17! Die Methode, die der junge Gauß für die 17-Teilung des Kreises entdeckt und mit der er die Mathematik zweier Jahrtausende in den Schatten gestellt hatte, erwies sich als unanfechtbar und allen Anforderungen an mathematische Exaktheit gewachsen. Gleichzeitig schuf der junge Entdecker aber auch eine abschließende Theorie der Kreisteilung, die das so lange und heiß umstrittene Problem mit einem Schlage bis in seine letzten Wurzeln erhellte. Auf Grund dieser Theorie ergab sich, daß jede Kreisteilung mit Zirkel und Lineal möglich ist, wenn die Teilungszahl eine Primzahl von der Form 2 ⁿ + 1 ist. Bei einer Primzahl dieser Form muß der Exponent n selbst wieder eine Potenz von 2, also eine der Zahlen 1, 2, 4, 8, 16, 32, 64 usw. sein. Setzen wir diese Zahlenwerte in den Ausdruck 2 ⁿ + 1 ein, so erhalten wir

2 ¹ + 1 = 3, also die 3-Teilung,
2 ² + 1 = 5, also die 5-Teilung,
2 ⁴ + 1 = 17, also die 17-Teilung,
2 ⁸ + 1 = 257, also die 257-Teilung,
2 ¹⁶ + 1 = 65 537, also die 65 537-Teilung.

Außer der 17-Teilung kamen also auch noch die 257- und die 65 537-Teilung, da diese Zahlen ebenfalls Primzahlen sind, zu den bis dahin bekannten Teilungsmöglichkeiten, ebenfalls alles höchst unglaubwürdige Zahlen, von denen bis dahin kein Mensch angenommen hätte, daß sie jemals in der Kreisteilung eine Rolle spielen würden. Aus der 17-Teilung ergab sich dann auch die 34-, 68- usw. Teilung, Entsprechendes für die anderen neuen Kreisteilungszahlen, und damit war man in der Lage, die Möglichkeit der Kreisteilung gewaltig zu bereichern und bis zu den fernsten Regionen der Zahlenreihe auszudehnen.

Allerdings haben die neuen Teilungsarten nur theoretisches Interesse. Schon die 17-Teilung mit Zirkel und Lineal ist eine höchst umständliche und mühevolle Arbeit und erfordert zu ihrer Ausführung bedeutende mathematische Kenntnisse; die 257-Teilung ist schon eine umfangreiche und in höchstem Maße komplizierte und zeitraubende Aufgabe, an die nur selten ein Gelehrter geht, und die 65 537-Teilung endlich ist bisher nur ein einziges Mal ausgeführt worden, und zwar von dem Mathematiker Hermes, der dafür nicht weniger als zehn voll Jahre brauchte. Die Ausführung dieser Konstruktion stellt ein gewaltiges Manuskript dar, das eine ganze große Kiste füllt und im Mathematischen Seminar der Universität Göttingen aufbewahrt wird.

Bemerkt sei noch, daß die Behandlung des Problems der 17-Teilung übrigens noch einen gewissen Fortschritt erreicht hat, und zwar insofern, als es gelungen ist, diese Konstruktion mit dem Zirkel allein, also mit Fortlassung des Lineals, auszuführen. Dem Franzosen L. Gerard gelang als erstem im Jahre 1896 diese Konstruktion, die also noch über die Platonische Bedingung hinausgeht.

Die Entdeckung der 17-Teilung des Kreises ist, wenn vielleicht auch nicht die bedeutendste, so doch zweifellos die genialste Leistung des unvergleichlichen Gauß. Er selbst hat diese Leistung wohl auch in dieser Weise eingeschätzt und den Wunsch geäußert, daß einst die symbolische Darstellung der 17-Teilung des Kreises seinen Grabstein schmücken möge. Dieser Wunsch ist erfüllt worden; auf dem Denkmal, das dem »Fürsten der Mathematiker« in seiner Geburtsstadt Braunschweig auf dem Gaußberg gesetzt worden ist, ist die 17-Teilung des Kreises plastisch dargestellt, um Kunde zu geben von der Tat eines jugendlichen Genies, die in ihrer Art völlig vereinzelt in der Geschichte der Wissenschaften dasteht und für immer ein Markstein in der Entwicklung der Mathematik und der Geschichte ihrer Probleme sein wird.

Postskriptum

Problematisch-mathematische Naturen – Der Kampf um die Siebenteilung – Eine Beinahe-Lösung – Entdeckerrausch – Ein winziger Unterschied – Enttäuschte Hoffnung – Eine kühne Analogie – Eine kleine Geschichte

Die Mathematik züchtet problematische Naturen! Freilich sind diese anderer Art als die Gestalten in Friedrich Spielhagens vielgelesenem Roman. Es sind das vielmehr jene Naturen, die, ohne zu den zünftigen Mathematikern zu gehören, dennoch Freude an den Problemen der so vielgeschmähten und doch so reizvollen Mathematik empfinden und den unbezähmbaren Trieb in sich spüren, das, was diese Wissenschaft für unmöglich erklärt, dennoch möglich zu machen. Die Quadratoren und Trisektoren gehören zu diesen Naturen, und zu ihnen gesellten sich, seit ich in einer weitverbreiteten Wochenschrift eine ähnliche wie die vorangegangene Abhandlung über die Kreisteilung veröffentlicht hatte, auch noch die Kreisteilungsproblematiker. Während über die Quadratur des Kreises und die Dreiteilung des Winkels, wohl auch über das Delische Problem, in den Zeitungen und Zeitschriften des öfteren geschrieben wird – notabene oftmals total Falsches und geradezu Unsinniges – werden die Probleme der Kreisteilung journalistisch so gut wie nicht ausgebeutet. Daher fand mein Aufsatz bei solchen wie den genannten problematischen Naturen einen ungeahnten Widerhall. Es war dort ausgeführt worden, daß es zwar viele Kreisteilungen gibt, die mit Zirkel und Lineal ausgeführt werden können, aber noch viel mehr andere, wie die Sieben-, Neun-, Elf-, Dreizehnteilung usw., bei denen das nicht der Fall ist, Konstruktionen, von denen die Mathematiker sogar behaupten, daß ihre exakte Ausführung unmöglich sei. Dieses »Unmöglich« erweckte das Problematische in der Natur vieler Leser, und viele, die sich, wenn auch widerstrebend, schon zu dem Zugeständnis durchgerungen hatten, daß man in der Frage der Quadratur des Kreises, der Dreiteilung des Winkels und der Verdoppelung des Würfels den Mathematikern, die diese Dinge für unmöglich erklären, vielleicht recht geben müsse, lehnten es ganz entschieden ab, dieses Zugeständnis auch auf die ihnen bekannt gewordene neue Unmöglichkeit auszudehnen. Schließlich können sich auch die Gelehrten irren, und selbst Mathematikern, sogar sehr bedeutenden, sind schon Irrtümer untergelaufen. Nur der eigene Versuch wirkt überzeugend, und viele, viele schrieben mir, aus In- und Ausland, daß sie durch eigene Versuche einen Irrtum der zünftigen Wissenschaft festgestellt und die für unmöglich erklärten Kreisteilungen mit mathematischer Exaktheit und nur mit Zirkel und Lineal möglich gemacht hätten, und sie sandten mir mehr oder weniger umfangreiche und komplizierte Konstruktionen, um mich von der Richtigkeit solcher kühnen Behauptung zu überzeugen. Da bekam ich reichlich zu tun, um die Mathematik gegen die Anfechtungen der problematischen Naturen zu verteidigen.

Die große Mehrzahl jener Versuche und Konstruktionen hatte es auf die Siebenteilung abgesehen, jenes uralte Problem, an dem schon die Geometer der alten Babylonier und Griechen ihren Scharfsinn erprobt hatten. Und in der Tat, es gibt eine Anzahl von Konstruktionen, die beinahe – aber freilich nur beinahe – die exakte Lösung dieses Problems sein könnten und meinen Widersachern recht zu geben schienen. Eine dieser Konstruktionen, die in dieser oder ähnlicher Form zur größeren Hälfte unter den mir übersandten Lösungsversuchen vertreten war, ist folgende: In einem Kreis wird, wie es die nebenstehende Figur 19 zeigt, ein Halbmesser halbiert und in dem Mittelpunkt desselben das Lot errichtet, alles Operationen, die mit Zirkel und Lineal wunderschön ausgeführt werden können. Wenn man dann die Strecke vom Fußpunkt des Lotes bis zur Kreislinie, also in unserer Figur die Strecke a, in den Zirkel nimmt und von einem beliebigen Punkte der Kreislinie an auf dieser hintereinander abträgt, so wird auf diese Weise die Kreislinie haarscharf in sieben Teile geteilt. Wer den Versuch mit der nötigen Genauigkeit macht, wird das Gesagte bestätigt finden. Der siebente auf diese Weise gefundene Zirkelpunkt fällt immer mit dem Ausgangspunkt zusammen, und selbst dem schärfsten Auge wird es kaum möglich sein, eine Abweichung zu konstatieren. Das ganze Verfahren erinnert natürlich an die Sechsteilung des Kreises, bei der durch Abtragung des Radius auf dem Kreisumfange dieser mit anerkannt mathematischer Exaktheit in sechs Teile geteilt wird.

Daher war es kein Wunder, daß viele Leser, die die beschriebene Konstruktion entdeckt hatten, damit die Lösung des Problems der Siebenteilung gefunden zu haben glaubten und in der felsenfesten Überzeugung von der Richtigkeit ihrer Konstruktion in ihren Briefen den ganzen Triumph der Entdecker ausströmen ließen. »An der Richtigkeit meiner Lösung ist nicht zu zweifeln!« schrieb mir in diesem Sinne ein Leser siegesbewußt. »Es ist mir am 9. Januar d. J., 12 Uhr nachts, gelungen, das Problem restlos zu lösen!« schrieb ein anderer, überzeugt, gut daran getan zu haben, daß er für etwaige spätere Forschungsarbeiten über den Werdegang seiner Entdeckung beizeiten das Datum dieser Großtat bis auf die Stunde genau fixierte. Ein anderer Leser und Löser sandte mir seine Photographie mit längerem Lebenslauf und dem höflichen, aber bestimmten Ersuchen, beides mitsamt seiner Lösung des Problems in der Zeitschrift, in der mein Aufsatz erschienen war, zu veröffentlichen, und für die Gewährung dieser Publikation hatte er sich ein beträchtliches Honorar ausbedungen. Andere meiner Problematiker hielten es aus Gründen der Vorsicht nicht für angebracht, mir ihre Lösungen mitzuteilen, sondern begnügten sich damit, mir die Tatsache ihrer Entdeckung zur Kenntnis zu bringen, und fragten gleichzeitig an, ob und wo und in welcher Höhe Preise auf die Lösung des Problems ausgesetzt seien, um die sie sich zu bewerben wünschten. Eine der übersandten Lösungskonstruktionen aber war mit drei verschiedenen Unterschriften unterzeichnet. Das hieß zu gut deutsch: Laß dir ja nicht einfallen, alter Freund, uns um die dir hiermit anvertraute Entdeckung zu bemausen und diese etwa als dein eigenes Geisteskind auszugeben; wir sind drei gegen einen und schwören dich nötigenfalls in Grund und Boden! Ein Schüler einer technischen Lehranstalt endlich sandte mir seine Konstruktion ein, versehen mit einem unterschriebenen und gestempelten Zeugnis des Leiters der Anstalt und des Inhaltes, daß die beifolgende Konstruktion zur Siebenteilung des Kreises mit dem Mikrometerzirkel nachgeprüft und ihre absolute Genauigkeit einwandfrei festgestellt sei! Man sieht, was die problematisch-mathematischen Naturen tun, das tun sie gründlich.

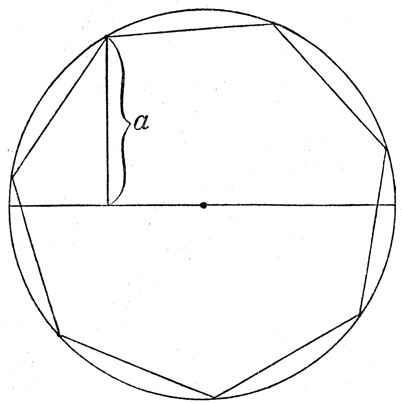
Abb. 19

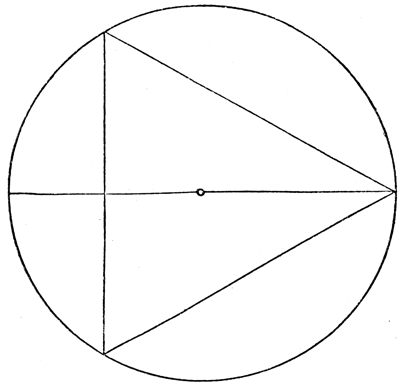
Abb. 20

Aber dieser Entdeckerrausch mußte gedämpft werden. Es tat mir beinahe leid, soviel Hoffnung zerstören zu müssen, aber die Wissenschaft über alles! Nun, die erwähnte Konstruktion zur Siebenteilung ist trotz ihrer anscheinenden Genauigkeit und trotz ihrer Ähnlichkeit mit der Sechsteilung doch keine wirklich genaue, sondern nur eine annähernde, sozusagen eine Beinahe-Lösung und war als solche auch den zünftigen Mathematikern keineswegs unbekannt. Die konstruierte Strecke a auf Abbildung 19 ist nämlich die mathematisch exakte Konstruktion der halben Seite des regelmäßigen Dreiecks. Wir hatten in der vorhergehenden Abhandlung bereits eine Konstruktion des regelmäßigen Dreiecks angegeben. Eine andere ist die folgende: Wenn auf dem Mittelpunkt des Kreisradius nach beiden Seiten eine Senkrechte errichtet wird und dann die beiden Schnittpunkte dieser Strecke mit der Kreislinie, so wie es Figur 20 zeigt, mit dem gegenüberliegenden Schnittpunkt des Durchmessers verbunden werden, so ist die so entstandene Figur das regelmäßige Dreieck, nach allen Regeln der Kunst mit Zirkel und Lineal ausgeführt und daher die mathematisch exakte Konstruktion desselben darstellend. Der Vergleich der beiden Figuren zeigt deutlich, daß die Strecke, mit der unsere Problematiker die Siebenteilung des Kreises gefunden zu haben glaubten, genau die Hälfte der Seite des regelmäßigen Dreiecks ist. Und diese Strecke ist zwar beinahe, aber doch nicht völlig gleich der Seite des regelmäßigen Siebenecks. Der Unterschied ist freilich nur ein ganz minimaler und beträgt, wie sich durch Rechnung ziemlich einfach feststellen läßt, nur etwa 17 Zehntausendstel des Radius des Kreises, also bei einem Kreise, dessen Halbmesser 1 Meter lang ist, nur 1,7 Millimeter, bei so kleinen Kreisen hingegen, wie man sie zu geometrischen Experimenten auf Papier zeichnet, nur etwa den zehnten oder hundertsten Teil eines Millimeters, und diese verschwindende Differenz war allen unseren siegesfrohen Problematikern entgangen, die hatte sich selbst mit dem Mikrometerzirkel nicht feststellen lassen.

Aber vorhanden ist diese Differenz, wie die Rechnung mit unumstößlicher Gewißheit ergibt, und selbst wenn sie noch millionmal kleiner wäre, so verhinderte sie dennoch, jene Konstruktion als mathematisch exakte Lösung anzuerkennen. Denn so klein auch jenes Stückchen ist, um das die wirkliche Seite des Siebenecks von der in obiger Weise konstruierten Strecke abweicht, so enthält sie doch immer noch unendlich viele Punkte, und es ist auf keine Art und Weise möglich, unter diesen den alleinigen und einzigen Punkt zu bestimmen, der die wirkliche Seite des Siebenecks begrenzt. Die Ausmessung mit dem Zirkel, auch mit dem Mikrometerzirkel, ist kein Beweis, denn der Zirkel soll lediglich zum Ziehen von Kreislinien dienen, ist aber kein Meß- und kein Beweisinstrument, und mikroskopisch kleine Abweichungen können wir selbst mit den schärfsten Meßapparaten nicht feststellen. Der exakte Beweis für die Richtigkeit einer solchen Behauptung oder Konstruktion kann eben immer nur erbracht werden, indem man die Behauptung auf die bekannten Grund- und Lehrsätze der Geometrie zurückführt, genau in der Weise, wie man etwa die Kongruenz von Dreiecken und daraus die Gleichheit von Seiten oder Winkeln beweist. Unsere Problematiker aber hatten sich durchweg mit dem Augenschein begnügt, der ihnen eine absolute Genauigkeit ihrer Konstruktion vortäuschte, einen wirklich einwandfreien Beweis hatte keiner von ihnen auch nur versucht. Das war ihre große Sünde gegen den Geist der Geometrie gewesen, die sie mit der Enttäuschung ihrer hochgeschwellten Erwartungen bezahlen mußten. »Grausame Ironie des Schicksals, das so große Annäherungen an die genaue Teilstrecke zuläßt, aber die ganz genaue Teilung verhindert!« so schrieb mir in diesem Sinne ein Leser, der mir seine Konstruktion zur Prüfung übersandt hatte, auf meinen Hinweis auf die bewußten siebzehn Zehntausendstel Differenz resigniert zurück.

Ein merkwürdiges Verfahren, um die Richtigkeit einer vorgenommenen Siebenteilung zu beweisen, hatte übrigens ein Problematiker weiblichen Geschlechtes, die Gattin eines Apothekers, angewandt. Die Dame hatte den geteilten Kreis mit möglichster Genauigkeit in sieben Sektoren zerschnitten und diese auf der Apothekerwaage ihres Gatten ausgewogen. »Die Wägung ergab absolute Gleichheit aller sieben Teile, und damit ist wohl der Beweis geliefert, daß mein Teilungsverfahren allen Anforderungen genügt!« schrieb mir dieser praktische Geometer. Dieser Schlußfolgerung konnte ich mich nun allerdings nicht anschließen, und weil das der Fall war und ich der Dame schrieb, daß die Waage, selbst die allerfeinste, kein Beweisinstrument für mathematische Zwecke sei und auch niemals Unterschiede von Millionstel oder Billionstel anzugeben imstande sei, bekam ich eine sehr deutliche Erwiderung, in der mir ob solcher »Haarspalterei« ganz gehörig der Text gelesen und für die Zukunft die unverhohlene Verachtung aller Mathematik ausgedrückt wurde.

Außer der beschriebenen wurden noch verschiedene andere Konstruktionen der Siebenteilung übersandt, und auch an der 9-, der 11- und der 13-Teilung versuchten sich viele Leser und Löser mit Scharfsinn und Verstand, aber natürlich alle ohne Erfolg. In allen Fällen ließ sich der Fehler, wenn er auch noch so minimal war, durch Rechnung mit unumstößlicher Gewißheit nachweisen, und damit wurden auch diese Hoffnungen zuschanden. Einem Leser jedoch konnte ich mit viel Freude die absolute Richtigkeit und Exaktheit seiner Konstruktion bestätigen. Er hatte in ähnlicher Weise, wie aus der 6- und der 10-Teilung des Kreises die 15-Teilung abgeleitet wird (im vorhergehenden Aufsatz ist das eingehend beschrieben), die 85-Teilung des Kreises gefunden. Und diese Konstruktion war vollkommen exakt und einwandfrei, nicht nur annäherungsweise. Aber, so mußte ich diesem Problematiker mitteilen, Neues hatte er mit seiner Entdeckung nicht zuwege gebracht. Denn die 85-Teilung ist aus der 5- und der 17-Teilung des Kreises ableitbar, in ähnlicher Weise auch die 51-Teilung aus der 3- und der 17-Teilung, was sich aus der Theorie der Kreisteilung ergibt. Wohl aber konnte ich diesem Leser zu dem Scharfsinn, den er bei der selbständigen Neuentdeckung dieser Teilungsart bewiesen hatte, meinen aufrichtigen Glückwunsch aussprechen.

Manche der Problematiker bekunden ihre Naturveranlagung übrigens auch in der Konstruktion kühner Analogien. Ist ihnen der Fehler ihres Lösungsversuches nachgewiesen, so kündigen sie alsbald neue an, die angeblich absolut fehlerlos sein sollen, und dem Einwand, daß Konstruktionen wie die 7- oder 11-Teilung des Kreises in exakter Weise nicht möglich seien, begegnen sie dann, indem sie sich für die Berechtigung ihres Strebens auf – Gauß berufen. Denn auch dieser habe die 17-Teilung des Kreises, die doch über zweitausend Jahre hindurch als unmöglich angesehen worden sei, schließlich dennoch möglich gemacht, warum sollte so Ähnliches nicht auch bei der angeblich unmöglichen 7- oder 11-Teilung gelingen?! Manche verwenden dieses Argument sogar, um auch für die Quadratur des Kreises oder die Dreiteilung des Winkels oder das Delische Problem noch Lösungsmöglichkeiten behaupten zu können. Man fühlt sich in der Verfolgung jener Probleme also als zweiter Gauß! Diese Analogie ist jedoch nur eine sehr oberflächliche. Denn wenn auch bis zu Gauß die 17-Teilung des Kreises nicht gelungen war, so hatte man doch auch keinen schlüssigen Beweis dafür aufgestellt, daß die Lösung dieser Aufgabe unmöglich wäre; das Problem war bis zu Gauß' Wirken durchaus in der Schwebe. Für die Quadratur des Kreises, die Dreiteilung des Winkels und die Verdoppelung des Würfels aber ist die Unmöglichkeit erwiesen, und zwar im wesentlichen durch die Arbeiten desselben Gauß, auf den sich jene Problematiker berufen. Ebenso hat die von Gauß aufgestellte Theorie der Kreisteilung, die zur Entdeckung der 17-Teilung führte, zugleich den Beweis der Unmöglichkeit für alle Teilungsarten erbracht, die, wie die 7-, 9-, 11- usw. Teilung, nicht der angegebenen Formel der Kreisteilungszahlen entsprechen. Also Vorsicht mit der Berufung auf Gauß!

Noch von einer kleinen hübschen Geschichte möchte ich erzählen, die sich an den obenerwähnten Aufsatz knüpft, wenn sie allerdings auch nur indirekt mit der Kreisteilung zu tun hat. Schrieb mir da auf diesen Aufsatz auch ein Leser, seines Zeichens Obertertianer vom Gymnasium in D., er habe meine Abhandlung über die Kreisteilung gelesen und daraus die Hoffnung und Überzeugung gewonnen, daß ich vielleicht auch imstande sei, ihn bei einer kniffligen mathematischen Aufgabe über den Kreis, die ihm sein Mathematiklehrer als Hausaufgabe zudiktiert habe, auf den rechten Weg zu bringen. Er komme nicht zustande damit, ob ich ihm daher nicht ein bißchen helfen wolle, und er bäte doch sehr darum, denn die Sache wäre für die kommende Versetzung von Entscheidung.

Nun, edel sei der Mensch, hilfreich und gut, und warum soll man einem bedrängten Obertertianer in Versetzungsnöten nicht ein wenig unter die Arme greifen? Erinnerungen an die eigene Tertianerzeit werden wach und bestärken den menschenfreundlichen Entschluß. Also schrieb ich ihm, gab ihm zwar nicht die Lösung der mitgeteilten Aufgabe selbst, wohl aber bestimmte Andeutungen, um den Charakter der Aufgabe und den Weg der Lösung zu erkennen.

Und der Erfolg solcher guten Tat? Nach drei Wochen hielt ich über ein Dutzend Briefe von Schülern des Gymnasiums in D. in Händen, aus allen Klassen von Tertia an aufwärts, und alle baten um freundlichen Beistand bei der Lösung der mitfolgenden mathematischen Aufgaben. Selbst zwei Herren Oberprimaner hatten mich mit ihrem Vertrauen beehrt zwecks Lösung einiger verwickelter stereometrischer Aufgaben. Da mußte ich nun freilich stoppen, denn erstens hätten es die mathematischen Kollegen vom Gymnasium in D. mit Recht wohl sehr übel vermerkt, wenn ihnen in solcher Weise in den geregelten Lehrplan hineingepfuscht worden wäre – natürlich vorausgesetzt, daß sie es herausgekriegt hätten, aber die Mathematiker kriegen ja bekanntlich alles heraus –, und zweitens hätte ich zu erwarten gehabt, daß, wenn sich die Sache weiter herumsprechen würde, alsbald weitere Gaue der gymnasialen deutschen Jugend mir ihr Vertrauen zuwenden würden und dann für den Rest meines Daseins meine Zeit und Arbeitskraft mit mathematischem Hilfsdienst vollkommen ausgefüllt worden wäre. Also mußte ich meinen jungen Freunden abschreiben, mit einem nassen und einem heiteren Auge, und ich hoffe, daß sie die angegebenen Gründe gewürdigt haben.