Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

7. Lösungen und Löser der »Heiteren Geometrie«

Nochmals: Apfelsine und Erdkugel – Anschauung und Denken – Fröhliche Wetten – Eine lustige Stammtischgeschichte – Die Korkkugel und der Athlet – Die Lösungen der Aufgaben – Der ordnungsgemäße Bücherwurm – Das Geheimnis der Schnalle – Eine überraschende Lösung

Auch die in dem vorangegangenen Aufsatz angeführten Fälle und Aufgaben aus dem Gebiet der Heiteren Geometrie sind von dem Verfasser mehrfach in Unterhaltungszeitschriften veröffentlicht worden. Die zahlreichen darauf erfolgten Zuschriften aus dem Leserkreis dieser Blätter sind ein hübscher Beitrag zu dieser heiteren Wissenschaft, weshalb einige dieser Zuschriften auch an dieser Stelle ehrenvolle Erwähnung finden sollen.

Zunächst war es jenes als Paradigma heiterer Geometrie angeführte Gedankenexperiment mit Apfelsine und Erdkugel, das den Forschungstrieb und – den Widerspruch vieler Leser weckte. Ein um die riesengroße Erdkugel gelegtes Band soll nach der Verlängerung um einen einzigen Meter denselben Abstand von der Kugeloberfläche ergeben wie das entsprechende Experiment mit einer Apfelsine. Diese Behauptung stieß, trotz der erläuternden Bemerkungen, in meinem Aufsatz, bei sehr vielen Lesern auf entschiedenen Unglauben. Die Anschauung der Leser konnte sich mit einem solchen merkwürdigen Verhalten der Kugel nicht einverstanden erklären und geriet zunächst mit den Behauptungen der Mathematik in einen unheilbaren Widerspruch. Unmöglich kann sich ein Band von einer Länge von 40 Millionen Metern ebenso verhalten wie ein Band von wenigen Zentimeter Länge, das war der Gedankengang, den jener Aufsatz bei allen diesen Lesern ausgelöst hatte und der sie veranlaßte, der Wahrheit durch das eigene Experiment auf den Grund zu gehen. Die Sache läßt sich ja ohne große Schwierigkeiten ausprobieren. Man braucht ja nicht gleich die Erdkugel selbst zu dem Experiment verwenden, sondern kann sich mit irgendwelchen größeren kreisrunden Gegenständen begnügen. Also ist damals, wie aus den Zuschriften meiner Leser hervorging, von ihnen viel praktische Kreisgeometrie getrieben worden, an Apfelsinen, an runden Tischen, an Schwung- und Wagenrädern, an Wasser- und sonstigen Türmen, und ein findiger Heidelberger hat sogar, wie er mitteilte, seine geometrischen Untersuchungen an dem weltberühmten großen Faß seiner Vaterstadt vorgenommen. Und zum Erstaunen aller Experimentatoren stimmte die bewußte Behauptung immer. Immer ergab sich der Abstand von 16 Zentimetern, wie klein oder wie groß auch das zu der Untersuchung verwandte Kreisgebilde war. Da mußte man ja schließlich jener Behauptung wohl Glauben schenken.

Aber freilich, ganz einleuchtend ist so manchem die Sachlage auch durch den Ausfall seines Experimentes nicht geworden, restlos war der Widerspruch zwischen Anschauung und mathematischem Ergebnis auch hierdurch nicht zu beseitigen. Daher wollen wir noch ein Vergleichsbeispiel anführen, das geeignet sein dürfte, die letzten leisen Zweifel zu beseitigen. Wir legen um ein Brett von – sagen wir – 10 Meter Länge ein Band in der Längsrichtung fest anliegend einmal herum. Dieses Band wird dann, wenn wir von der Dicke des Brettes absehen, eine Länge von 20 Metern haben. Verlängern wir dieses Band um einen Meter und legen es dann, zu einer Schleife verknüpft, wieder in der Längsrichtung des Brettes gleichmäßig um dieses herum, so wird das Band an jedem Ende des Brettes um % Meter überragen. Ohne weiteres einleuchtend ist es nun, daß es ganz gleichgültig ist, ob ich zu diesem Experiment ein Brett von 10 oder 1000 oder 1 000 000 Meter Länge verwende. Der Überschuß muß in allen Fällen dasselbe ¼ Meter betragen, und damit haben wir endlich auch anschaulich den Beweis, das bei solchen Bandexperimenten der Überschuß des um 1 Meter verlängerten Bandes von der Größe des verwandten Versuchskörpers vollständig unabhängig ist. Und wenn man sich in ähnlicher Weise die Sache auch noch an einer Kiste veranschaulicht – die entsprechenden Maßgrößen lassen sich leicht berechnen –, so wird endlich auch dem hartnäckigsten Zweifler in anschaulichster Weise klar werden, daß sich in unserem Gedankenexperiment die Erdkugel genau so, wie angegeben, verhalten muß und sich gar nicht anders verhalten kann.

Eine Reihe von Lesern, die sich auf solche Weise schließlich von der Richtigkeit des Gesagten überzeugt hatte, hat dann die so gewonnene Erkenntnis schnöderweise benutzt, um höchst erfolgreiche Wetten abzuschließen, natürlich mit Leuten, denen die Sache noch nicht bekannt war und die jene Behauptung absolut nicht glauben wollten. Wenn dann die angestellten Meßexperimente die Richtigkeit jener Behauptung ergaben, gab es immer einen fröhlichen Gewinner und einen sehr überraschten Verlierer. So schrieb mir Dr. Z. in Dresden, daß er auf solche Weise von einem ungläubigen Patienten einen vollen Korb Sekt gewonnen habe, und Fräulein v. R. schrieb freudestrahlend, daß sie auf ähnliche Weise dem Herrn Papa, der absolut nicht an die Richtigkeit jener geometrischen Behauptung glauben wollte und erst durch umständliche Meßversuche an dem kreisrunden Gartenbeet zu ihrer Anerkennung veranlaßt werden konnte, endlich das bis dahin immer vergeblich gewünschte funkelnagelneue Fahrrad abgewonnen habe und seitdem eine begeisterte Anhängerin der Geometrie geworden sei. Herr Hotelbesitzer M. im Oldenburgischen aber gewann auf diese Weise von einem befreundeten Gutsbesitzer drei Sack Kartoffeln; aber der Verlierer rächte sich und schickte dem Gewinner die größten Kartoffeln, die auf drei Meilen im Umkreise aufzutreiben waren, mit entsprechenden begleitenden Zeilen ins Haus! Wer wollte da noch an dem Humor der Mathematik zweifeln?

Zu katastrophalen Folgen aber hätte unser Gedankenexperiment beinahe in der guten Stadt P. geführt. Dort hatte ein Stammtischgenosse die Geschichte von der Erdkugel und der Apfelsine gelesen und den übrigen Mitgliedern der Runde zum Besten gegeben. Entschiedener Widerspruch gegen die Richtigkeit des Gehörten wurde ringsum laut. Also mußte die Probe auf das Exempel gemacht werden. Eine Apfelsine brachte der Stammtischwirt bald zur Stelle, und mit einem Bindfaden ward die Messung vorgenommen. Dann wurde das Experiment an dem kreisrunden Stammtisch ausgeführt und schien die Richtigkeit des Versuchs zu ergeben. Aber einige Genossen der Runde waren auch jetzt noch nicht ganz bekehrt. Dazu müßte, so meinten sie, der Versuch noch an einem weiteren und viel größeren runden Körper vorgenommen werden. Aber woher einen solchen nehmen? Da erinnerte man sich des kreisrunden Brunnenbeckens auf dem Marktplatz, das wohl an zehn Meter im Durchmesser haben mochte, und alsbald machte sich die ganze Stammtischrunde auf den Weg, um sich trotz der vorgerückten Stunde am Brunnen Wahrheit und Gewißheit zu holen. Mit dem großen Bindfadenknäuel und mit Hallo und Gelächter machte man sich an die Ausmessung des Brunnenbeckens. Dieses ungewohnte nächtliche Tun aber erweckte den Argwohn des beamteten Wächters der Nacht, der in einer Haustürnische gerade den gewohnten Mitternachtsschlaf zu halten gedachte, nunmehr aber voller Mut und Amtseifer sich wie ein Indianer an die mit dem langen Bindfaden experimentierende Gesellschaft heranschlich. In strengem Ton heischte er Aufklärung über das nächtliche Tun, worauf man ihm einen längeren Vortrag über die geometrischen Beziehungen zwischen einer Apfelsine und dem Erdball hielt. Sei es aber, daß das Auge des Gesetzes die Geschichte mit der Apfelsine für eine Verulkung der hohen Obrigkeit hielt, sei es, daß er die Apfelsine, die einer der Herren noch immer krampfhaft in der Hand hielt, für eine Bombe mit anarchistischem Daseinszweck ansah, kurz und gut, er erklärte, die Hand griffbereit an der polizeilichen Waffe, die gesamte fidele Stammtischrunde für verhaftet und ersuchte stramm und streng, ihm auf die Wache zu folgen. Mit Wonne kamen die Stammtischler der freundlichen Aufforderung nach in dem erhebenden Gefühle, daß sich hier ein Spaß von ungeahnten Dimensionen vorbereite. Nun, und auf der Polizeiwache löste sich die Sache denn auch bald in Wohlgefallen auf. Die Apfelsine wurde seziert und erwies sich als harmlose Südfrucht und keine Bombe; der Aufsatz über das Experiment mit Erde und Apfelsine wurde vorgelesen und damit bewiesen, daß das angestellte Experiment tatsächlich nur der Erforschung der Wahrheit dienen sollte und keinerlei staatsgefährlichen Charakter hatte. Also trennte man sich schließlich mit Lachen und Händeschütteln von dem Orte des Gesetzes und hielt dann im Stammlokal noch einen längeren Nachtschoppen. Zwei Tage daraus aber stand im Lokalblatt ein Artikel mit geheimnisvollen Andeutungen über ein beabsichtigtes Attentat auf den Marktbrunnen mit Bomben in Apfelsinenformat; die Attentäter seien bekannt und die Polizei entfalte die bekannte fieberhafte Tätigkeit. Der Stammtisch aber hatte wochenlang Stoff zum Lachen und hat mir die Geschichte zum Dank dafür getreulich berichtet.

Dann hat auch die in dem vorangegangenen Aufsatz ebenfalls zu einem Gedankenexperiment verwandte Korkkugel von 4 Meter Durchmesser damals den Lesern Stoff zu heiteren Untersuchungen über die Geometrie gegeben. Eine ganze Anzahl von Lesern schrieb, daß nicht nur sie selbst über das Gewicht von 10 000 Kilogramm einer solchen Kugel im höchsten Maße verblüfft waren, sondern auch viele ihrer Bekannten in den gleichen Zustand der Verblüffung versetzt hätten. Zumeist wurde immer auf ein Gewicht von »etwa einem halben Zentner« oder höchstens einem Zentner geraten, und auch hier hat der wirkliche Tatbestand mehrfach zu lustigen Wetten Anlaß gegeben. So teilte mir ein Leser aus München mit, daß er einem Freunde, einem bekannten Amateurathleten, eine Wette angeboten habe, daß dieser eine Korkkugel von der bezeichneten Größe nicht zu heben vermöge. Der starke Mann habe die Wette hohnlachend angenommen und sich anheischig gemacht, besagte Korkkugel mindestens ein dutzendmal zu stemmen. Als er dann das Nettogewicht einer solchen Kugel erfahren habe, sei er allerdings zunächst stumm vor Staunen gewesen, aber geistesgegenwärtig habe er sich auf den Standpunkt gestellt, daß die Wette nur in der Weise wirklich ausgetragen werden könne, daß zunächst einmal eine Korkkugel jener Dimension beschafft würde. Darauf hätten sich die Herren an eine Korkwarenfabrik gewandt, die auch durchaus bereit gewesen sei, eine solche Kugel herzustellen, aber zunächst einmal eine Anzahlung von fünfundzwanzigtausend Mark gewünscht habe, und weil der Wettgegner dieses Kapital nicht investieren wollte, so habe er trotz der Richtigkeit seiner Behauptung die Wette verloren und für den ganzen Athletenverein den Silvesterpunsch bezahlen müssen.

Lassen wir nunmehr die Lösungen der im vorangegangenen Aufsatz angeführten Aufgaben folgen.

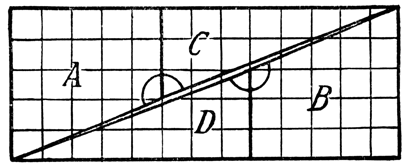
Abb. 32

Aufgabe 1. Die Verwandlung einer Fläche von 64 Quadratzentimeter Inhalt durch bloßes Zerschneiden in eine solche von 65 Quadratzentimeter ist natürlich nur scheinbar und beruht auf einer allerdings raffinierten Ungenauigkeit. Die vier Teile, in die die Figur 24 zerschnitten worden ist, lassen sich nämlich nicht ganz so exakt, wie es die Figur 25 zeigt, aneinanderlegen. Die schräge Linie von A ist nicht die genaue geradlinige Verlängerung der schrägen Linie von C, sondern die beiden Linien bilden zusammen einen stumpfen Winkel, dessen beide Schenkel eine zwar nahezu, aber doch nicht genau gerade Linie bilden, und dasselbe gilt auch von B und D. Die nebenstehende Figur 32, die die Teile in exakt aneinandergelegter Form zeigt, läßt das gut erkennen; an den Stellen der beiden Kreisbogen liegen die stumpfen Winkel. Die beiden Schräglinien von A und C bzw. B und D bilden daher nicht die genaue Diagonale des Rechteckes, sondern diese vier Linien schließen einen leeren Raum in Form eines langgestreckten Parallelogramms ein, dessen Inhalt gerade das eine Quadratzentimeter darstellt, um das die Figur 25 größer ist als die Figur 24, aus der sie entstanden war. Die Ungenauigkeit ist allerdings nur eine ganz geringe, und wer das interessante Experiment anstellt, ist zunächst geneigt, die Ungenauigkeit auf eine solche des Scherenschnittes zurückzuführen. Erst wenn die Figur ganz genau gezeichnet wird und die vier Teile ebenso genau geschnitten und aneinandergelegt werden, tritt die Ursache der absonderlichen Inhaltsvermehrung in Erscheinung.

Aufgabe 2. Viele Leser werden die Länge der Bohrstrecke mit 20 Zentimeter angegeben haben; wer vorsichtiger war, hat noch 4 Millimeter für zwei Buchdeckel in Abzug gebracht und ist auf 19,6 Zentimeter gekommen. Beide Angaben sind aber falsch; der Bücherwurm hat vielmehr nur die geringe Strecke von 4 Millimeter durchbohrt, um zu seinem Ziele zu kommen. Denn bei zwei ordnungsmäßig nebeneinanderstehenden Büchern liegt die erste Seite des Bandes neben der letzten Seite des zweiten Bandes, und beide Seiten sind nur durch die beiden Umschlagdeckel voneinander getrennt, wie jedermann an irgend zwei nebeneinanderstehenden Bänden feststellen kann. Der Bücherwurm hatte daher nur die beiden trennenden Buchdeckel zu durchbohren, die zusammen 4 Millimeter stark sind.

Auch die Lösung dieser Aufgabe hat einer Anzahl kritischer Leser zu denken gegeben. Ihre Richtigkeit wurde beanstandet mit der Begründung, daß die Bohrstrecke nur unter der Voraussetzung 4 Millimeter betrage, daß die Bücher in der Reihenfolge von links nach rechts aufgestellt werden; werden die Bücher dagegen von rechts nach links aufgestellt, so habe sich der Bohrwurm durch die ganze Dicke der beiden Bücher durchzufressen, und es sei nicht einleuchtend, daß eine solche Aufstellung der Bücher nicht auch »ordnungsgemäß« sei. Darauf ist zu bemerken, daß wir, wie wir von links nach rechts schreiben, so auch die Zahlen von links nach rechts folgen lassen und daher auch bei der Einrichtung unserer Bibliotheken die numerierten Bände in dieser Reihenfolge anordnen müssen. Nur eine Bücherordnung nach diesem Prinzip kann daher Anspruch auf das Prädikat »ordnungsgemäß« erheben. Ein Leser schrieb, daß er sich tatsächlich entschlossen habe, seine umfangreiche Bibliothek umzuordnen, weniger um den Bücherwürmern zu imponieren, sondern weil nach seiner Meinung eine Bibliothek nur dann »ordnungsgemäß« eingerichtet sei, wenn die letzte Seite jedes Bandes sich neben der ersten des folgenden Bandes befinde. Nun, man soll die Konsequenz nicht übertreiben und auch dem Bücherwurm weiterhin sein verblüffendes Kunststück gönnen.

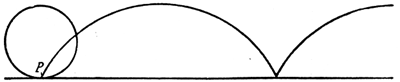
Abb. 33

Aufgabe 3. Die Lösung dieser Aufgabe erfordert ein gewisses Vermögen der Veranschaulichung, wenn sie richtig ausfallen soll. Oft wird eine Art zurücklaufender Schleifenlinie oder auch eine Schlangenlinie als der Weg bezeichnet, den der fragliche Punkt zurücklegt. Das ist jedoch nicht richtig. Stellt in der nebenstehenden Figur 33 der Kreis den Umfang eines Wagenrades dar, und ist P der Punkt, dessen Weg festgestellt werden soll, so beschreibt dieser beim Fahren eine Reihe von Bogenlinien in der Form und Aufeinanderfolge, wie es die Figur veranschaulicht. Diese Bogenlinie, die also an keiner einzigen Stelle zurückläuft, heißt Radlinie oder Zykloide und spielt in der höheren Geometrie eine sehr wichtige Rolle. Auch diesen Vorgang kann man experimentell ausführen, indem man eine kreisrunde Pappscheibe vor einer Wand auf einer Kante rollen läßt und dabei an der Wand den Weg, den ein bestimmter Punkt am Umfang der Scheibe zurücklegt, markiert.

Aufgabe 4. Diese Aufgabe ist etwas kniffliger Natur und erfordert zu ihrer Lösung eine genaue Betrachtung des Falles, die dann den Widerspruch der aufgestellten Behauptung klarlegt. Wenn die Scheibe A sich einmal vollständig abrollt, dann ist die Strecke AA so lang wie der Umfang der Scheibe A. Gleichzeitig mit A rollt auch die Scheibe B auf der Strecke BB ab. Die Länge dieser Strecke ist aber nicht gleich dem Umfang der Scheibe B, denn diese führt bei ihrer Bewegung von links nach rechts auf der Strecke BB nicht nur eine Roll-, sondern gleichzeitig auch eine Gleit- oder Schleifbewegung aus. Soviel als die Strecke BB größer ist als der Umfang der Scheibe BB, kommt hierbei auf Rechnung der Gleitbewegung. Deutlich wird das, wenn wir uns die Bewegung des Mittelpunktes M der Scheiben veranschaulichen. Dieser hat natürlich überhaupt keinen Umfang und legt dennoch bei vollständiger einmaliger Abrollung der Scheibe A eine Strecke zurück, die ebenfalls so groß ist wie AA oder BB. Der Punkt M führt also überhaupt keine Roll-, sondern nur eine Gleitbewegung aus. Die Scheibe A macht nur eine Rollbewegung; alle Scheiben bzw. alle Kreise, die kleiner als A sind, vollführen gleichzeitig eine Roll- und eine Gleitbewegung, so daß also die zurückgelegte Strecke nur in dem Falle der Scheibe A so lang wie der Umfang der Scheibe ist.

Aufgabe 5. Diese Aufgabe ist geeignet, selbst Mathematiker stutzig zu machen, denn die Anwendung der erwähnten Lehrsätze ist durchaus korrekt. Durch bloßes Nachdenken über die Anwendung jener Lehrsätze wird man, wenn man diese Dinge nicht sehr perfekt beherrscht, den Fehler kaum finden, sondern erst, wenn man dazu übergeht, die ganze Konstruktion der Figur nochmals genau mit Zirkel und Lineal zu wiederholen. Dann stellt sich heraus, daß die Figur eine Ungenauigkeit enthält. Die Strecken AE und AD gehen nämlich in Wahrheit nicht durch die Mittelpunkte der beiden Kreise, sondern sind etwas verschoben. Bei korrekter Ausführung der Konstruktion geht die Verbindungslinie DE durch den unteren Schnittpunkt der beiden Kreise, so daß dann überhaupt kein Dreieck mehr entsteht, also auch keins mit einer Winkelsumme von mehr als zwei rechten Winkeln. Die vorgenommene kleine Schiebung wird zumeist nicht sofort bemerkt, besonders dann nicht, wenn man die Aufgabe vorführt und dabei die Kreise mit freier Hand zeichnet, die Konstruktion also nur andeutet, wobei man die kleine Ungenauigkeit sehr geschickt verhüllen kann.

Aufgabe 6. Die Querlinien in den Figuren 28 und 29 sind überhaupt nicht gebogen, sondern sind gerade und parallel und haben überall gleichen Abstand. Sie stellen einen sehr interessanten Fall optischer Täuschung dar; ihre Biegung wird durch die eingezeichneten Strahlenbündel vorgespiegelt.

Aufgabe 7. Die Aufgabe wird gelöst, indem man beispielsweise an dem obersten Punkte der Figur beginnt, nach links geht und jedesmal, bevor man ein Dreieck schließt, zum nächstfolgenden übergeht. Man kommt dann zu einem Punkte, von dem aus man die Schließung der einzelnen Dreiecke vornehmen kann. Nach einiger Übung wird die Lösung gelingen. Die Aufgabe ist nicht schwer und dient eigentlich nur zur Vorbereitung auf die

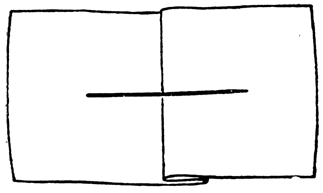
Abb. 34

Aufgabe 8. Diese Aufgabe dürfte von allen diejenige gewesen sein, die unseren Lesern und Lösern am meisten zu schaffen gemacht hat, denn sie ist ihrer ganzen Natur nach dazu angetan, einen Menschen stundenlang zu beschäftigen. Pfundweise Papier kann man mit dem Versuche, die Aufgabe zu lösen, vollzeichnen, und die merkwürdigsten Konstruktionen und Hilfsmittel, wie doppelte Bleistifte, Bleistifte mit doppelter Spitze usw., werden ersonnen, um auf des Pudels Kern zu kommen, der sich aber dennoch dem Scharfsinn selbst der ausdauerndsten Löser entzieht. Nach mehr oder weniger langem vergeblichen Bemühen kommt man dann meist zu der Überzeugung, daß die Lösung der Aufgabe unmöglich sei. Dem kann jedoch nicht ganz zugestimmt werden. Die Lösung der Aufgabe ist möglich, allerdings nur durch einen kleinen »Kniff«, und Zwar durch einen Kniff in des Wortes buchstäblichstem Sinne. Man knifft nämlich das Blatt, auf dem die Zeichnung ausgeführt werden soll, doppelt, wie es die nebenstehende Abbildung 34 veranschaulicht, und zieht dann über die Knifflinie einen geraden Strich. Faltet man das Blatt dann auseinander, so teilt sich der ursprüngliche, in einem Zug hergestellte Strich in zwei einzelne, in gleicher Richtung liegende Striche. Mit zwei weiteren Zügen ist dann die vollständige Zeichnung herzustellen, wie es die Abbildung 35 veranschaulicht, bei der die Verbindungslinien absichtlich ungeschlossen geblieben sind, um den Weg der Züge zu zeigen. Die Aufgabe ist ein ganz vorzügliches Unterhaltungsspiel und geeignet, ganze Gesellschaften stundenlang zu beschäftigen. Meist ertönt schon sehr bald nach Inangriffnahme der Freudenruf: »Ich hab's!«, darauf aber immer sehr bald und kleinlaut der Enttäuschungslaut: »Ach nein!«, weil sich herausgestellt hat, daß doch noch ein kleines Stück an der verlangten Zeichnung fehlt. Und so pflegt das stundenlang zu gehen, jedesmal fehlt immer gerade noch ein kleines Stück. Auf andere als die hier angegebene Weise ist die Aufgabe nicht zu lösen. Ob freilich die Lösung mit dem »Kniff« eine ganz korrekte ist, sei der Beurteilung des Lesers anheimgestellt. Maßgebende Instanzen bestreiten es leider, und deswegen konnte auch der oben erwähnte Preis, der auf die korrekte Lösung der Aufgabe einstmals ausgesetzt war, nicht gewonnen werden.

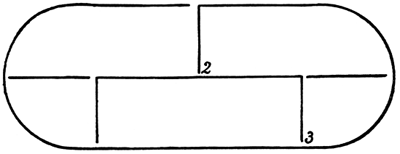
Abb. 35

Die Schnallenaufgabe dürfte jedenfalls unseren Lesern viel Stoff zu geometrischen Versuchen geliefert haben und hat auch nach einer früheren Veröffentlichung unter allen geometrischen Kuriositäten den Vogel abgeschossen, nach Zahl und Inhalt der damals eingegangenen Zuschriften zu schließen. Der Versuch, die Aufgabe zu lösen, hat zu tiefgründigen geometrischen Forschungen angeregt. Mit doppeltem und ausgezacktem Bleistift, mit Pauspapier und Zaubertinte ist man dem Ding zu Leibe gegangen, und eine Reihe von Lesern hat die angegebene Lösung auch selbständig gefunden. Viele andere freilich, denen die Lösung nicht geglückt war, haben dann, als die Lösung bekanntgegeben worden war, aus ihrem Herzen keine Mördergrube gemacht und mir mehr nachdrücklich als liebenswürdig bestätigt, daß ich allen Anlaß habe, hinsichtlich dieser Aufgabe und ihrer Lösung ein schlechtes Gewissen zu haben. Ein Leser hat sogar klar und deutlich »Schieber« geschrieben, dann aber versöhnend hinzugesetzt, daß ihm die Sache riesigen Spaß gemacht habe. Denn er habe die Aufgabe der bei ihm am Silvesterabend versammelten Freundesrunde beiderlei Geschlechts aufgegeben. Mit Feuereifer habe man sich an die Lösung gemacht, stundenlang daran gearbeitet und beinahe darüber vergessen, zur Mitternachtsstunde auf das neue Jahr anzustoßen. Noch weit ins neue Jahr hinein habe man an der Figur »herumgeknobelt« und eine Unmasse Papier und Bleistift verbraucht; erst in früher Morgenstunde des neuen Jahres habe man erschöpft den Kampf um die Lösung aufgegeben und sich unter feierlichen Verwünschungen des Urhebers der heiteren Geometrie getrennt. Ich habe das deutlich gemerkt, denn gerade um jene Zeit hat mein rechtes Ohr wie eine Weckeruhr geklingelt.

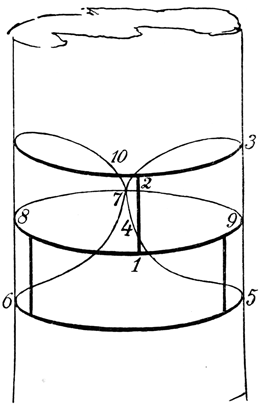
Abb. 36

Eine sehr hübsche und überraschende Lösung der Aufgabe aber hat ein Leser gefunden, der die Schnalle mit Kreide auf ein – Ofenrohr gezeichnet hatte, und zwar derart, daß die beiden seitlichen Enden der Schnallenfigur sich berühren, was auf der gekrümmten Fläche des Ofenrohres möglich ist. Es entsteht dann die nebenstehende Figur (Abbildung 36), die unsere Schnalle in perspektivischer Zeichnung auf dem Ofenrohr darstellt. Auf diese Art ist es möglich, die ganze Figur mit Ausnahme der beiden unteren vertikalen Striche in einem Zuge zu zeichnen, etwa indem man den Linienzug in der durch die Zahlen in der Figur angedeuteten Weise beginnt und weiterführt. Die beiden unteren Vertikalstriche erfordern dann noch zwei Züge, und damit ist die ganze Figur in drei Zügen hergestellt. Freilich, ganz korrekt ist auch diese Lösung nicht, aber sie ist eine neue und originelle Note unter den zahllosen Lösungsversuchen, die mir im Laufe der Jahre unterlaufen sind, und macht den Scharfsinn ihres Erfinders alle Ehre.