Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

6. Heitere Geometrie

Aus dem Kuriositätenkabinett der Mathematik – Apfelsine und Erdkugel – Ein merkwürdiges Ergebnis – Anschauung und Denken – Das Möbiussche Blatt – Die Aufgaben

Wie die Wissenschaft von den Zahlen ihre heitere Seiten hat, so auch jenes Gebiet der Mathematik, das von den räumlichen Größen handelt, also die Geometrie. Auch hier gibt es vieles, das selbst den geschworenen Feind der Mathematik interessant und humorvoll anmutet und ihn zur Beschäftigung reizen kann, und ebenso entbehrt auch dieses Gebiet nicht zahlreicher Scherzaufgaben, die auf Trugschlüsse oder Paradoxien hinauslaufen und einen manchmal recht erheblichen Grad von Scharfsinn erfordern, wenn es gelingen soll, auf den Kern des Problems zu kommen. Meistens verhält es sich bei den Kuriositäten in geometrischem Gewande übrigens so, daß der humorvoll anmutende Charakter nur die äußere Seite eines im übrigen durchaus ernsten und eigenartigen Problems darstellt, ohne daß der Liebhaber solcher Aufgaben das immer vollständig erfaßt. Gerade die Geometrie liefert viele und überaus interessante Beiträge zu dem Kuriositätenkabinett der Mathematik, die zwar ein gewisses Verständnis für die Welt der räumlichen Größen verlangen, im übrigen aber aus dem Rahmen der üblichen Schulgeometrie sehr herausfallen. Die nachfolgenden Beispiele werden das Gesagte vollauf bestätigen.

Zunächst wollen wir uns mit einer höchst merkwürdigen Eigenschaft der Kugel befassen, von der keiner unserer Leser etwas in der Schule gehört hat, denn sie ist sogar manchen Mathematikern von Fach nicht bekannt. Zu diesem Zweck wollen wir das folgende Gedankenexperiment machen. Wir denken uns eine Apfelsine (die wir ja als annähernd kugelförmig betrachten können) und um diese festanliegend ein Band herumgelegt. Dann verlängern wir dieses Band um einen Meter, knüpfen es an den Enden zusammen und legen es konzentrisch, das heißt wie einen Kreis, um die Apfelsine. Zwischen Kugeloberfläche und Kreisband wird dann ein gewisser Abstand vorhanden sein, der schätzungsweise etwa 16 Zentimeter beträgt, was der Leser leicht feststellen kann, denn das Experiment kann ja ohne weiteres ausgeführt werden. Nun wollen wir in Gedanken dasselbe Experiment auch mit der riesengroßen Erdkugel anstellen. Wir denken uns also zunächst wieder ein Band festanliegend um den Erdball gelegt; dieses Band hat eine Länge von 40 Millionen Meter. Dann verlängern wir auch dieses Band um einen einzigen Meter, was angesichts der ungeheuren Länge des Bandes natürlich nur eine ganz winzige Verlängerung bedeutet. Das so verlängerte Band denken wir uns dann wieder konzentrisch um die Erdkugel herumgelegt. Auch in diesem Falle wird das so verlängerte Band einen gewissen Abstand von der Oberfläche der Erdkugel haben, und wir stellen unseren Lesern nunmehr die Frage: Wie groß wird in diesem Falle der Abstand des Bandes von der Kugeloberfläche sein? Wird dieser Abstand so groß sein, daß man vielleicht den kleinen Finger zwischen Band und Kugel hindurchstecken kann? Ausgeschlossen! wird die Antwort lauten. Oder könnte dann vielleicht eine Mücke hindurchkriechen? Auch noch ausgeschlossen! wird man sagen, denn bei der ungeheuren Größe des Erdumfanges bzw. bei der Länge des Bandes von 40 Millionen Meter kann eine Verlängerung um einen einzigen Meter keinen überhaupt merkbaren Abstand zwischen Kugel und Band bewirken. Aber vielleicht könnte wenigstens ein Bazillus da hindurchkriechen, denn ein solches Lebewesen soll ja nur den millionsten oder milliardsten Teil eines Millimeters dick sein? Der könnte vielleicht zwischen Band und Kugel hindurchkriechen, vorausgesetzt, daß er sich sehr dünn macht und sich nicht beschwert, wenn er etwas gequetscht werden sollte! so wird man nach einiger Überlegung vielleicht antworten.

Denjenigen unserer Leser, die in dieser oder ähnlicher Weise die gestellte Frage beantworten, müssen wir aber erwidern, daß ihre Antworten total falsch sind. Denn der Abstand des Bandes von der Kugeloberfläche ist auch im Falle der Erdkugel groß genug, um nicht nur den kleinen Finger, sondern auch die ganze Faust, ja sogar eine ganze Katze in Lebensgröße hindurchzulassen, denn er ist genau so groß wie im Falle der Apfelsine und beträgt wie in diesem Falle etwa 16 Zentimeter. Diese Behauptung wird den meisten unserer Leser, die das Gedankenexperiment mitgemacht haben, als einfach lächerlich oder total unglaubwürdig erscheinen, zum mindesten wird es eine sehr große Überraschung bedeuten. Und nicht nur Laien, selbst Mathematiker, denen das Experiment unbekannt ist, werden durch das Ergebnis in vielen Fällen verblüfft sein. Denn unsere Anschauung scheint dem mitgeteilten Ergebnis völlig zu widersprechen und läuft immer wieder darauf hinaus, daß bei der ungeheuren Länge eines Bandes von 40 Millionen Meter die Verlängerung um die verhältnismäßig ganz winzige Größe von einem einzigen Meter unmöglich einen solchen großen Abstand bewirken kann. Bei der Apfelsine ist die Verlängerung von einem Meter mehrmals so groß wie das ursprüngliche Band selbst, bei der Erdkugel beträgt sie nur den 40millionsten Teil des ursprünglichen Bandes, da kann doch unmöglich in beiden Fällen derselbe Abstand herauskommen! Und dennoch ist es so. Die Anschauung trügt in diesem Falle, oder wir verbinden sie irrtümlicherweise mit unserem Gedankenexperiment. Denn der Abstand ist von der Größe der Kugel vollständig unabhängig und beträgt in allen Fällen dieselben ungefähren 16 Zentimeter, gleichviel ob wir das Experiment mit einer Apfelsine oder mit der Erdkugel oder selbst mit einer noch millionenmal größeren Kugel, etwa der Sonnenkugel, anstellen.

Dem Leser, der sich mit unserer Behauptung nicht abfinden kann, raten wir, zu seiner Überzeugung das Experiment praktisch an Kugelkörpern oder Kreisen von verschiedener Größe anzustellen, zuerst also an einer Apfelsine, dann etwa an einem Kürbis oder Globus, auch ein Faß oder eine kreisrunde Tischplatte, die ja immerhin schon einen zwanzig- oder dreißigmal größeren Durchmesser als eine Apfelsine haben, können dazu herhalten, und wer will, kann sich auf dem Erdboden einen beliebig großen Kreis aufzeichnen. In allen Fällen wird er nach Verlängerung des ersten Bandes um einen Meter feststellen können, daß der Abstand jedesmal der gleiche ist, und dann wird er jedenfalls schon eher geneigt sein, dieses Ergebnis auch für den Fall der Erdkugel gelten zu lassen. Denjenigen unserer Leser jedoch, die aus ihrer Schulzeit her noch über die Kenntnis der Kreisrechnung verfügen, können wir in leichterer Weise die Überzeugung von der Richtigkeit jener Behauptung vermittels des mathematischen Beweises verschaffen. Der Umfang eines Kreises oder einer Kugel ist bekanntlich abhängig von dem Radius ( r) und beträgt immer 2 × r × π (wo π die bekannte Zahl 3,1415 … usw. ist). Die Länge des festanliegenden Bandes ist also in allen Fällen 2 × r × π Meter. Verlängere ich dieses Band um 1 Meter und lege dieses dann konzentrisch um die Kugel, so erhalte ich einen neuen Kreis von 2 × r × π + 1 Meter Umfang. Der Radius dieses neuen Kreises aber beträgt dann Meter.

Der Unterschied zwischen dem Radius des ersten Kreises und dem des Kreises mit vergrößertem Umfang beträgt also in allen Fällen ¹/ _2π Meter, was ungefähr 16 Zentimeter ausmacht, und dieser Unterschied stellt immer den Abstand des verlängerten Bandes von der Kugeloberfläche dar. Wir sehen aber zugleich auch, daß die Größe ¹/ _2π konstant, das heißt in allen Fällen dieselbe und von dem Radius der Kugel vollständig unabhängig ist, denn dieser kommt in dem Ausdruck ¹/ _2π ja überhaupt nicht vor. Für den Mathematiker ist damit der Fall bewiesen, aber selbst die so gewonnene theoretische Überzeugung verhindert nicht, daß man sich kopfschüttelnd fragt, wieso die Anschauung diesem Ergebnis zunächst immer so entschieden Widerspruch leistet. Unser Gedankenexperiment mit der Kugel erweist sich dadurch, daß es in dem naiven Bewußtsein immer eine so völlige Diskrepanz zwischen der Anschauung und dem wirklichen Sachverhalt bewirkt, als eine der eigenartigsten Proben aus dem Kuriositätenkabinett der Mathematik.

Noch ein anderes Kugelexperiment wollen wir anstellen. Kork ist bekanntlich eine sehr leichte Substanz und ein Flaschenkork beispielsweise wiegt, wie man zu sagen pflegt, »so gut wie nichts«. Wie schwer wird dann wohl eine Korkkugel von vier Metern Höhe, also etwa Zimmerhöhe, sein? Als Antwort auf diese Frage wird das Gewicht einer solchen Korkkugel zumeist mit 20 bis 30 Pfund angegeben. Vorsichtige Leute allerdings äußern sich, daß eine solche Kugel doch nicht so leicht sein könne, wie es den Anschein habe, und raten auf einen oder einige Zentner Gewicht. In Wirklichkeit aber wiegt eine solche wie die angegebene Korkkugel rund 10 000 Kilogramm, also volle 200 Zentner, was dem Ladegewicht eines Güterwagens entspricht. Auch hier geraten Anschauung und Wirklichkeit zunächst in einen Widerstreit. Das Bewußtsein, daß Kork eine ganz leichte Substanz ist, verführt dazu, auch einer Korkkugel von der genannten Größe nur ein verhältnismäßig niedriges Gewicht zuzuschreiben. Es wird jedenfalls, wenn es eben nur geschätzt und nicht exakt berechnet wird, immer viel zu niedrig angegeben. Auch hier führt erst die Berechnung des Kubikinhaltes der Kugel, der rund 33 Kubikmeter beträgt, und die Berücksichtigung des spezifischen Gewichtes des Korks (0,3) zu dem richtigen Ergebnis, das dann auch immer eine Überraschung bedeutet.

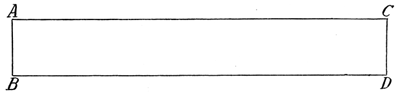
Abb. 22

Ein höchst eigenartiges Experiment geometrischer Natur ist ferner auch das folgende: Wir nehmen einen Hohlkörper, etwa einen Zylinder, den wir uns aus Papier leicht herstellen können (mit oder ohne Deckflächen) und schneiden an irgendeiner Stelle dieses Zylinders mit der Schere hinein. Wenn wir den Schnitt jetzt so führen, daß er zu seinem Ausgangspunkte zurückkehrt, so wird der Zylinder natürlich in zwei Teile geteilt. Dasselbe ist der Fall, wenn wir das Experiment mit irgendeinem anderen Hohlkörper, etwa einer Kugel, einem Würfel oder sonstigem Gebilde, anstellen. Immer wird der Körper durch einen solchen vollständigen, das heißt zu seinem Ausgangspunkt zurückführenden Schnitt in zwei getrennte Teile geteilt; ebenso verhält es sich auch bei einem Blatt Papier, wenn wir auf diesem einen solchen Schnitt vollführen, und unserer Anschauung nach muß das bei jedem Körper der Fall sein, mit dem wir ein solches Experiment anstellen. Fragen wir nun, ob sich der Leser vielleicht einen Körper denken kann, der dieser Behauptung widerspricht, der also durch einen vollständigen Schnitt nicht in zwei voneinander getrennte Teile zerfallen würde, so wird die Antwort jedenfalls nein lauten, und das war lange Zeit auch die Ansicht der Mathematiker. Daher war es eine große Überraschung, als in der Mitte des vorigen Jahrhunderts der Mathematiker Möbius ein geometrisches Gebilde bekanntgab, bei dem jenes Experiment zu einem anderen Ausfall führt. In unserer Abbildung 22 ist ein Rechteck gezeichnet mit den Seiten AB und CD. Der Leser möge sich ein solches Rechteck aus Papier schneiden und die beiden Ränder so aufeinanderkleben, daß die Ecke A auf D und die Ecke B auf C fällt, was durch eine Verdrehung des Papierstreifens möglich ist. Es wird dann ein Gebilde von der Form der Abbildung 23 entstehen.

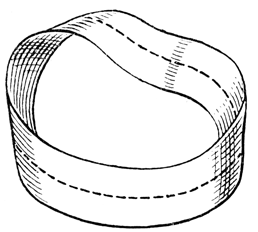
Abb. 23

Wird nun von irgendeiner Stelle des Streifeninnern aus ein Schnitt in der Längsrichtung des Streifens so geführt, daß er zu seinem Ausgangspunkt zurückkehrt (die gestrichelte Linie in der Figur zeigt die Richtung eines solchen Schnittes), so wird man die merkwürdige Entdeckung machen, daß der Streifen trotzdem nicht in zwei Teile zerfällt, sondern nach wie vor ein einziges zusammenhängendes Band darstellt. Auch der Ausfall dieses Experimentes scheint aller Anschauung zu widersprechen und wirkt dadurch höchst verblüffend. Als dieses Gebilde – es heißt nach seinem Entdecker das Möbiussche Blatt – und dessen merkwürdige Eigenschaften bekannt wurden, bedeutete das für die Mathematiker selbst eine Überraschung. Bis dahin hatte es gleichsam als ein Axiom gegolten, daß ein jeder Flächenkörper durch einen vollständigen Schnitt in zwei Teile zerfallen müsse, und das Bekanntwerden des Möbiusschen Blattes nötigte, den hierauf bezüglichen geometrischen Sätzen eine veränderte Fassung zu geben.

Wir erwähnten bereits, daß auch die Geometrie Scherzaufgaben kennt, die zu Trugschlüssen oder Paradoxien führen oder auch in anderer Hinsicht überraschende Resultate ergeben. Einige solcher Kleinprobleme heiterer Geometrie wollen wir nunmehr folgen lassen. Sie setzen (mit Ausnahme der Aufgabe 5) keine eigentlichen geometrischen Kenntnisse voraus, sondern verlangen nur etwas Scharfsinn und die Fähigkeit zur Veranschaulichung einfacher räumlicher Verhältnisse oder Vorgänge und überraschen dann durch die Eigenart ihrer Resultate.

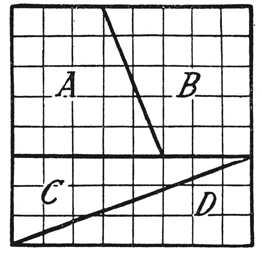
Abb. 24

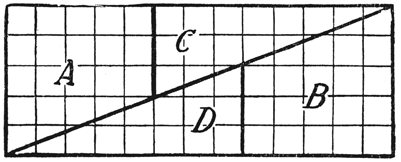
Abb. 25

Aufgabe 1. Vermittels der beiden Figuren 24 und 25 kann bewiesen werden, daß 8 × 8 = 65 ist. Die Figur 24 stellt ein Quadrat von 8 Zentimeter Seitenlänge dar (es ist hier in verkleinertem Maßstabe wiedergegeben), sein Flächeninhalt ist also 8 × 8 = 64 Quadratzentimeter. Wir zerschneiden nun das Quadrat in der in der Figur durch die starken Striche angedeuteten Weise in vier Einzelteile, also in die beiden Trapeze A und B sowie die beiden Dreiecke C und D. Diese Einzelteile lassen sich zu der Figur 4 zusammenlegen; die Art der Zusammenlegung ist auch hier aus den starken Strichen ersichtlich. Diese Figur aber stellt ein Rechteck mit einer Seite von 13 und einer von 5 Zentimeter Länge dar; der Inhalt dieser Figur ist also 5 × 13 = 65 Quadratzentimeter. Es stellt sich also das überraschende Ergebnis heraus, daß lediglich durch Zerschneiden der Figur der Quadratinhalt derselben vermehrt worden ist oder daß 8 × 8, das nach Figur 24 = 64 ist, nach der anders zusammengelegten Figur = 65 ist. Wie ist das möglich?

Aufgabe 2. In einem Bücherregal stehen nebeneinander Band I und Band II eines wissenschaftlichen Werkes. Es sind zwei stattliche Folianten, jeder über 1000 Seiten stark und jeder gerade 10 Zentimeter dick. Die Stärke des Umschlagdeckels werde dabei mit je 2 Millimeter angenommen. Ein Bücherwurm, d. h. ein richtiger aus dem Insektenreich, hat sich von der ersten Seite des ersten Bandes bis zur letzten Seite des zweiten Bandes in gerader Linie durchgebohrt. Wie groß ist die Strecke, die er durchbohrt hat?

Aufgabe 3. Wir betrachten an einem Wagenrad den tiefsten Punkt des Rades; das ist der Punkt, mit dem das Rad den Erdboden berührt. Was für eine Linie beschreibt dieser Punkt, wenn sich der Wagen in Bewegung setzt?

Abb. 26

Aufgabe 4. Es kann bewiesen werden, daß alle Kreise gleichen Umfang haben, wie groß auch ihr Durchmesser sei. Zu diesem Zwecke betrachten wir die Figur 26, die eine kreisrunde Scheibe A darstellt, auf der eine kleinere Scheibe B sitzt. Der Mittelpunkt beider Scheiben ist der gemeinsame Punkt M, beide Scheiben sind fest miteinander verbunden. Wir lassen nunmehr die Scheibe A einmal auf der Linie AA abrollen; die Strecke AA ist dann natürlich gleich dem Umfang des Kreises A. Gleichzeitig mit der Scheibe A dreht sich dann auch die Scheibe B, und hat A, auf der rechten Seite angelangt, hier eine volle Umdrehung vollzogen, so hat das auch die Scheibe B getan. Die Linie BB ist dann die Roll-Linie der Scheibe B, die also dem Umfang von B entsprechen muß. Die Strecke BB aber ist, wie aus der Figur ohne weiteres ersichtlich ist, genau so lang wie die Strecke AA, und damit ergibt sich, daß die beiden Kreisscheiben A und B trotz ihres verschiedenen Durchmessers den gleichen Umfang haben. Stimmt es oder stimmt es nicht?

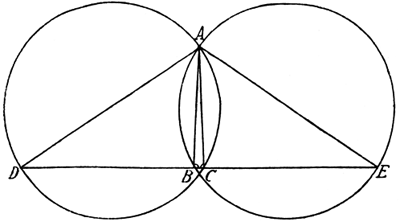
Abb. 27

Aufgabe 5. Der wichtigste Fundamentalsatz der ebenen Geometrie, der jedem Schüler schon in den ersten Wochen der Beschäftigung mit dieser schönen Wissenschaft haarscharf bewiesen und nachdrücklichst eingeprägt wird, lautet, daß die Summe der Winkel in jedem Dreieck gleich zwei rechten Winkeln ist. Auf diesem Satz baut sich ein großer Teil der gesamten ebenen Geometrie überhaupt auf, und seine Erschütterung wäre geradezu eine Katastrophe für die Mathematik und noch mehr für die Mathematiker. Trotzdem sind wir in der Lage, ein Dreieck anzugeben, bei dem die Summe der Winkel größer als zwei Rechte ist. Zu diesem Zweck betrachten wir die Figur 27, zu deren Verständnis lediglich die elementarsten Kenntnisse aus der Geometrie erforderlich sind. Sie stellt zwei Kreise dar, die sich zum Teil überschneiden. Von dem einen der beiden Schnittpunkte, A, aus legen wir die Durchmesser AD und AE durch die Mittelpunkte der beiden Kreise; dann verbinden wir die Punkte D und E durch eine Gerade, die die beiden Kreise in den Punkten B und C schneidet. B und C verbinden wir dann noch mit A, wodurch das Dreieck ABC entsteht. Dann ist nach dem Satz des Thales der Winkel bei B ein rechter Winkel, weil er Peripheriewinkel im Halbkreise ABE ist, und ebenso ist auch der Winkel bei C ein rechter als Peripheriewinkel im Kreise ACD. Dann hat also das Dreieck ABC bei B und C je einen rechten Winkel und überdies noch bei A einen kleinen spitzen Winkel. Die Summe seiner Winkel ist mithin um den kleinen Winkel A größer als zwei rechte. Quod erat demonstrandum! Diese Aufgabe ist ein besonderer Leckerbissen für Freunde der Geometrie. Wer unternimmt es, die drohende katastrophale Erschütterung der Geometrie, die aus dem merkwürdigen Dreieck ABC spricht, abzuwenden?

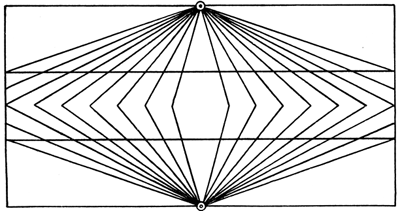
Abb. 28

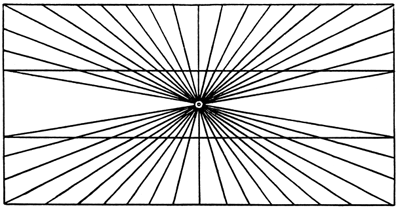
Abb. 29

Aufgabe 6. Wo haben die gebogenen Querlinien der Figur 28 und ebenso die der Figur 29 ihren größten Abstand? In der Mitte oder an den Seiten?

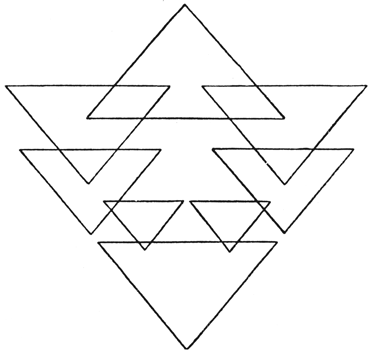
Abb. 30

Aufgabe 7. Die Figur 30 soll in einem Linienzug gezeichnet werden, selbstverständlich ohne unerlaubte Hilfsmittel wie doppelten Bleistift o. ä. und ohne ein Linienstück doppelt zu ziehen.

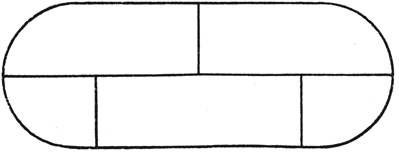
Abb. 31

Aufgabe 8. Die Figur 31, die etwa eine Schnalle darstellen könnte, soll in drei Zügen gezeichnet werden, selbstverständlich ebenfalls ohne eine Linie doppelt zu ziehen. Wer die Aufgabe 7 gelöst und die Figur 30 nach Vorschrift herausbekommen hat, wird vielleicht der Meinung sein, daß die soviel einfachere Figur 31, für die überdies drei Züge zulässig sind, doch keinerlei besondere Schwierigkeiten verursachen kann. Er wird sein blaues Wunder erleben, wenn er sich an die Lösung dieser Aufgabe macht. Auf die korrekte Lösung dieser Aufgabe war vor Jahren einmal ein hoher Preis ausgesetzt.

Mit diesen acht Aufgaben wollen wir es genug sein lassen des interessanten Spiels mit den Gesetzen der Geometrie. Sie dürften den Lesern ausreichende Beschäftigung und zugleich die Möglichkeit scharfsinniger und teilweise nicht ganz leichter Untersuchungen über räumliche Beziehungen und Vorgänge darbieten. Wir lassen die Lösungen der Aufgaben folgen, doch raten wir auch in diesem Falle, die Lösungen keinesfalls vorwegzunehmen, sondern sie erst nach erfolgten eigenen Lösungsversuchen mit den gefundenen Ergebnissen zu vergleichen.