
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Der goldene König – Der geheimnisvolle Hundertmarkschein – Was ist ein Kuß? – Eisenbahn und Rechenkunst – Schach dem Turm! – Das gerettete »volle Glas Bier« – Mathematik am Stammtisch – Flasche und Kork
Aufgabe 1. Die Lösung dieser Aufgabe sieht sehr leicht aus, dennoch ist zu befürchten, daß sich eine Anzahl der Leser die Sache noch leichter gemacht hat, als sie ist, indem sie einfach 75 × 2800 Mark = 210 000 Mark als Resultat der Aufgabe errechnet haben. Aber so billig wäre König Midas, nachdem er in pures Gold verwandelt worden war, doch nicht zu haben gewesen. Im Normalzustande, als er noch aus Fleisch und Bein bestand, wog er 75 Kilogramm, nach seiner Verwandlung in Gold aber wog er 19mal mehr, denn das spezifische Gewicht des Goldes ist 19mal größer als das durchschnittliche spezifische Gewicht der Körpersubstanz des Menschen. Also bezifferte sich der Wert des Gold gewordenen Königs auf 75 × 2800 × 19 = 3 990 000 Mark, ein Resultat, das wohl nicht jeder Löser der Aufgabe errechnet hat.
Gegen diese Lösung ist wiederholt der Einwand erhoben worden, daß bei der Verwandlung des Körpers Seiner Majestät des Königs Midas das angegebene Gewicht von 75 Kilogramm durchaus erhalten bleibe, wenn mit der Verwandlung zugleich auch eine Verringerung des Körpervolumens auf den neunzehnten Teil stattfinde, und eine solche Verringerung besage die Aufgabe implizite. Dem kann aber mit guten Gründen widersprochen werden. Der Begriff der Verwandlung enthält keinesfalls zugleich den der Volumenverringerung, und die meisten Leser und Löser werden sich zweifellos den in Gold verwandelten König auch nach seiner Verwandlung in voller Lebensgröße vorgestellt haben. Es kam bei der Aufgabe darauf an, das Moment des spezifischen Gewichtes, das die Aufgabe selbst nicht erwähnt, zu entdecken und in die Rechnung miteinzubeziehen; für eine Volumenverringerung lag nach Sinn und Wortlaut der Aufgabe keine Veranlassung vor.
Aufgabe 2. Der Schaden des Juweliers beträgt 100 Mark. Denn er selbst hat bei dem Geschäft zunächst 100 Mark eingenommen, nämlich die 100 Mark, die ihm der gefällige Nachbar für den falschen Hundertmarkschein gab, hat selbst aber fortgegeben das Armband im Werte von 60 Mark, die 40 Mark, die er dem faulen Kunden bei dem Kauf noch bar herausgab, und endlich die 100 Mark, die er dem Nachbar erstatten mußte, zusammen 200 Mark, so daß er bei dem Geschäft 100 Mark eingebüßt hat, nicht mehr und nicht weniger. Trotzdem wird der Schaden des Juweliers oftmals auch anders angegeben, und nach einer Veröffentlichung dieser Aufgabe in einem Unterhaltungsblatt erhielt ich mehrere Dutzend von Zuschriften, in denen die mitgeteilte Lösung für falsch erklärt wurde. Mit merkwürdiger Übereinstimmung rechneten die meisten der Einsender mir vor: Wert des gelieferten Armbandes 60 Mark; herausgegebenes Wechselgeld 40 Mark; Einlösung des falschen Hundertmarkscheines 100 Mark, macht zusammen 200 Mark! Wer hat also recht? Nun, der Widerspruch ist ohne Schwierigkeit zu lösen. Alles, was in jener Gegenrechnung angeführt worden ist, stimmt, nur haben die Herren Kritiker vergessen, die 100 Mark in Rechnung zu stellen, die der Juwelier von dem gefälligen Nachbarn für den falschen Schein erhalten hatte. Diese 100 Mark von dem eben berechneten Betrage von 200 Mark in Abzug gebracht, bleiben wiederum nur 100 Mark Schaden des Juweliers übrig; es wird beim besten Willen nicht mehr. In ähnlicher Weise rechnen andere Opponenten immer einen Posten zuwenig oder zuviel. Der Direktor einer Aktiengesellschaft rechnete mir haarscharf vor, daß der Schaden des Juweliers 140 Mark betrage, und ein Einsender gab das Höchstgebot mit 360 Mark angeblichen Schadens des Juweliers ab. Man kann übrigens die Lösung der Aufgabe auch gänzlich ohne Rechnung, auf rein logischem Wege, finden, wenn man sich folgendes vergegenwärtigt: Wäre der Hundertmarkschein echt gewesen, so hätte der Juwelier natürlich überhaupt keinen Schaden gehabt, also kann sein Schaden natürlich nur so groß sein wie der Nominalbetrag des falschen Hundertmarkscheins. Oder man kann auch schließen: Der diebische Käufer hat bei der Sache gerade 100 Mark, nämlich das Armband von 60 Mark und 40 Mark bar, ergattert, und mehr als dieser durch Betrug sich angeeignet hat, kann natürlich der Schaden des Betrogenen nicht sein. Manche Unzufriedene endlich halten der Lösung noch entgegen, daß der Schaden des Juweliers weniger als 100 Mark betragen habe, weil davon der Verdienst, der in dem Verkaufspreis von 60 Mark für das Armband eingerechnet ist, in Abzug gebracht werden müsse. Auch dieser Einwand ist nicht stichhaltig, denn der Juwelier hat durch den Diebstahl nicht nur das, was ihm das Armband selbst gekostet hat, sondern natürlich auch den Verdienst verloren, den er bei regulärem Verkauf des Stückes erzielt haben würde. Also, es bleibt bei den 100 Mark Schaden!
Aufgabe 3. Die Summe 1 + 2 + 3 beträgt 6, das Produkt 1 × 2 × 0 × 3 aber ist = 0, denn jedes Produkt, in dem auch nur ein Faktur Null ist, ist im ganzen Null. Den Glauben an die Richtigkeit dieses Resultates konnte einst ein Einsender nicht aufbringen, der mir schrieb: Wenn ich jemandem erst einmal, dann zweimal, dann dreimal und schließlich noch nullmal hinter die Ohren haue und der Verhauene mich dann bei Gericht anzeigt, glauben Sie, daß mich dann das Gericht freisprechen wird mit der Begründung, daß ich den anderen überhaupt nicht verhauen habe!? Hierzu wurde dem Zweifler geantwortet: Nein, Verehrtester, Sie werden wegen körperlicher Mißhandlung nach Recht und Rechenkunst verknackt; denn Sie haben dem anderen eine und zwei und drei Ohrfeigen, zusammen sechs Ohrfeigen, versetzt. Sie haben die Ohrfeigen addiert und nicht multipliziert, und auf die Addition hat die Null keinen Einfluß, auch beim Ohrfeigengeplänkel nicht. Aber vielleicht bekommen Sie wegen arithmetischer Unkenntnis Bewährungsfrist, wenn die Sache nicht mit Geld abzumachen ist!
Aufgabe 4. Die Lösung dieser Aufgabe wird zumeist mit 100 oder 90 Küssen angegeben, was aber beides falsch ist. Beim Abschied gibt zunächst die erste Dame jeder der anderen neun einen Kuß, gibt also 9 Küsse, und geht, wie wir der besseren Veranschaulichung wegen annehmen wollen, aus dem Zimmer. Von den zurückbleibenden neun Damen gibt wiederum eine den übrigen acht je einen Kuß, gibt also 8 Küsse; die nächste kann nur noch 7 Küsse vergeben, und so kommt eine Summe von 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 Küsse heraus, keiner mehr, aber auch keiner weniger.
An die Veröffentlichung dieser Aufgabe in einer weitverbreiteten Wochenschrift schloß sich einst eine sehr heitere Polemik an über die Richtigkeit des Resultates. Reichlich zwei Dutzend Leser, und zwar durchweg Damen, schrieben mir dieserhalb und bestritten die Richtigkeit des Resultates, das nach ihrer Meinung mit 90 Küssen anzugeben sei. Das Argument der einen Partei war: Damen küssen sich gegenseitig nur auf die Wangen, nicht auf die Lippen, und bei dieser Art des Küssens kommen 90 Küsse heraus, da hierbei ein gegebener Kuß von dem Empfänger immer an den Spender zurückgegeben wird. Das wäre an und für sich richtig, gilt aber eben nur für Wangenküsse; in der Aufgabe ist aber von Küssen schlechtweg, nicht von Wangenküssen, die Rede, und wenn man von Küssen ohne weiteren Zusatz redet, so ist nach allgemeinem deutschen Sprachgebrauch immer der Lippenkuß gemeint, und damit ist die Anzahl der 45 Küsse, die bei jener Prozedur herauskommt, gerechtfertigt. Schwieriger war ein anderes Argument, das übereinstimmend von einer ganzen Anzahl der Einsenderinnen zu diesem Thema in folgender Form vorgebracht wurde: Wie Druck immer Gegendruck erzeugt, so ein Kuß auch immer einen Gegenkuß; wenn sich also zwei Menschen einen Kuß geben, so sind das in Wirklichkeit zwei Küsse, denn es gibt hierbei nicht nur der eine dem anderen, sondern auch der andere dem ersten einen Kuß. Auf diese Weise kämen dann 90 Küsse statt der berechneten 45 heraus. Über diese Frage, also ob ein Kuß, den sich zwei Menschen geben, in Wirklichkeit zwei Küsse seien – und über diese Frage läßt sich von logischen Gesichtspunkten aus durchaus und mit Recht streiten –, konnten die feindlichen Parteien trotz wiederholter Replik und Duplik lange Zeit hindurch nicht zu einer Einigung gelangen, bis sich schließlich die Anhängerinnen der Zwei-Kuß-Theorie folgender vergleichender Argumentation beugten: Wenn das Ehepaar Meier ein Kind hat, so kann man sagen: Herr Meier hat ein Kind und Frau Meier hat ein Kind; das ist aber doch nur ein Kind, denn das Kind, das Herr Meier hat, ist dasselbe Kind, das Frau Meier hat. Ebenso ist es, wenn sich das Ehepaar Meier einen Kuß gibt. Dann kann man auch sagen, Herr Meier gibt Frau Meier einen Kuß, und Frau Meier gibt Herrn Meier einen Kuß. Das sind aber doch nicht zwei Küsse, denn der Kuß, den Herr Meier der Frau Meier gibt, ist derselbe Kuß, den Frau Meier Herrn Meier gibt, ist also nur ein Kuß. Gegen diese »Meierei« war nicht anzukämpfen, weder logisch noch arithmetisch, und so verblieb es bei den 45 Küssen.
Aufgabe 5. Diese Aufgabe wird voraussichtlich von vielen der Leser als schwer empfunden worden sein, vielleicht sogar als schwerer, als es dem Charakter der heiteren Rechenkunst entspricht. Die Mathematiker unter den Lesern werden die Aufgaben vielleicht sogar in die Form einer unendlichen Reihe gebracht haben, zu der sie ihrer Art nach allerdings sehr geeignet zu sein scheint. Aber das ist durchaus überflüssig, denn die Aufgabe ist, rein rechnerisch betrachtet, spielend leicht und kaum schwieriger als die andere Eisenbahnaufgabe, die wir als Probebeispiel angeführt hatten, nur muß sie ebenfalls logisch richtig angefaßt werden, was dann zu der folgenden sehr einfachen Folgerung führt: Da die beiden Züge zu derselben Zeit abfahren und auch die gleiche Geschwindigkeit haben, müssen sie sich gerade in der Mitte der Strecke, also nach 400 Kilometern Fahrt, treffen. Da sie mit 50 Kilometer Geschwindigkeit fahren, erreichen sie den Treffpunkt gerade in acht Stunden. Ebenso lange hat aber nach der Aufgabe die Taube zu fliegen, und da diese in der Stunde 60 Kilometer zurücklegt, so hat sie im ganzen 480 Kilometer zu fliegen. Was sehr einfach zu beweisen war.
Die Lösung dieser Aufgabe ist bisher nicht beanstandet, dagegen konnte sich ein Einsender mit der Lösung der anderen, als Beispiel gegebenen Eisenbahnaufgabe, die von den beiden Zügen handelt, die gleich weit von Berlin entfernt sind, wenn sie sich treffen, nicht einverstanden erklären, und er schrieb ironisch, daß ich mich hierbei gehörig »verdacht« habe. Zum Beweise dessen sandte er eine Zeichnung, ein Doppelgleis darstellend, auf dem die beiden Züge so weit einander genähert sind, daß die Stirnlinien der Lokomotiven eine Linie bilden. Bei dieser Stellung wäre tatsächlich der eine Zug um eine volle Zuglänge von irgendeinem in der Gleisrichtung liegenden Punkte weiter entfernt als der andere. Aber wie kann man denn bei einer solchen Stellung der beiden Züge von einem »Treffen« derselben reden? Es treffen sich hierbei lediglich die Stirnlinien der Lokomotiven, während von einem wirklichen Treffen der beiden Züge erst dann gesprochen werden kann, wenn die Züge sich ihrer ganzen Ausdehnung nach auf den beiden Gleisen gegenüberstehen, also ihre Mittelpunkte zusammenfallen oder doch auf einer Linie, senkrecht zum Gleise, liegen. Dann aber sind beide Züge von jedem Ort auf der Gleisstrecke gleich weit entfernt, und davon beißt keine Maus einen Faden ab.
Aufgabe 6. Das Schachbrett hat bekanntlich 64 Felder. Steht nun der weiße Turm auf irgendeinem Felde, so kann der schwarze Turm auf 63 anderen Feldern stehen. Auch zu jeder anderen Stellung des weißen Turmes kann der schwarze Turm jedesmal 63 verschiedene Stellungen einnehmen. Da der weiße Turm nun im ganzen auf 64 verschiedenen Feldern stehen kann, so können beide Türme im ganzen 64 × 63 = 4032 verschiedene Stellungen zueinander einnehmen. Die Richtigkeit dieser Lösung wird manchmal angezweifelt; es wird behauptet, daß von den angegebenen 4032 Stellungen alle diejenigen in Abzug zu bringen seien, in denen nach den Regeln des Schachspiels der eine Turm den anderen schlagen könne. Dazu ist zu bemerken, daß in der Aufgabe lediglich nach der Zahl der möglichen Stellungen der beiden Türme zueinander gefragt worden ist. Dazu gehören aber auch die Schlagstellungen, denn auch diese sind nach den Schachregeln möglich und kommen überdies in jeder Partie vor. Es liegt also keinerlei Veranlassung vor, diese Stellungen aus der Zahl der möglichen Stellungen auszuscheiden.
Aufgabe 7. Der Eisenbahnwagen wird durch die Ladung nicht schwerer, sondern – leichter. Denn um den Wagen mit dem Wasserstoffgas füllen zu können, muß zunächst die Luft aus ihm entfernt werden. 50 Kubikmeter Luft aber wiegen etwa 50 Kilogramm, die 50 Kubikmeter Wasserstoffgas aber nach der Angabe der Aufgabe nur etwa 5 Kilogramm, so daß der Wagen nach der Füllung um 45 Kilogramm leichter ist als vorher. Hier liegt also der Fall vor, wo, im eisenbahntechnischen Sinne wenigstens, ein Wagen im beladenen Zustande leichter ist als im unbeladenen.
Aufgabe 8. Daß das Fahrzeug für dieselbe Strecke und bei gleicher Geschwindigkeit einmal 1 Stunde 20 Minuten, das andere Mal nur 80 Minuten benötigt, erklärt sich daraus, daß 1 Stunde 20 Minuten = 80 Minuten ist, ein Faktum, das, so banal es ist, nichtsdestoweniger durch die Art, wie die Aufgabe gestellt wird, oftmals übersehen wird, weil wir immer im Dezimalsystem zu denken und zu rechnen gewohnt sind und 1,20 etwas anderes ist als 0,80. Gerade Leute, die viel rechnen, fallen deswegen mit Vorliebe auf diese Scherzaufgabe herein und geben die merkwürdigsten Gründe für den angeblichen Unterschied an, während mehr naiv veranlagte Gemüter den Scherz sofort durchschauen.
Aufgabe 9. Wir hoffen, daß denjenigen unserer Leser, die Freunde eines guten Glases Bier, notabene eines vollen Glases, sind, der Schreck über die merkwürdige Gleichung, derzufolge zwischen einem vollen und einem leeren Glas Bier eigentlich kein Unterschied ist, nicht allzusehr in die Glieder gefahren ist. Es sei ihnen allen zum Troste gesagt, daß jene sonderbare Rechnung gottlob einen Fehler enthält, zwar keinen Rechenfehler, wohl aber einen Denkfehler, der obendrein nicht einmal ganz leicht ausfindig zu machen ist. Ein »halbvolles« Glas Bier ist nämlich etwas ganz anderes als ½ volles Glas Bier. Jenes ist ein ganzes Bierglas, das nur zur Hälfte gefüllt ist und tatsächlich ebensogut als halbleer bezeichnet werden kann; ½ volles Glas Bier hingegen ist die mit Bier gefüllte Hälfte eines ehemals ganzen Bierglases, also etwa eines Glases, das in mittlerer Höhe quer durchgeschnitten ist, und ½ leeres Glas ist ein solches halbiertes Bierglas in leerem Zustande. Also darf ich aus der Tatsache, daß ein halbvolles Glas Bier auch als halbleer bezeichnet werden kann, keinesfalls die Gleichung herleiten ½ volles Glas Bier = ½ leeres Glas Bier, womit das erschreckende Resultat in nichts verfliegt. Es lag also in der Rechnung eine Verwechslung der sehr verschiedenen Begriffe »Glas Bier« und »Bierglas« vor. Zu diesem Ergebnis schrieb mir einmal ein Leser sehr launig, daß er doch schwere Bedenken gegen diese Lösung der Aufgabe habe und er es für seine Person vorziehe, um der Sache ordentlich auf den Grund zu gehen, längere Zeit hindurch einmal volle und halbvolle Gläser auszuprobieren, um sich wirklich zu überzeugen, daß leer und voll nicht dasselbe seien. Manchmal scheine ihm das wirklich so zu sein, aber das läge wohl nur daran, daß die Wirte jetzt das Bier so furchtbar »schnitten«, so daß man zwischen leer und voll schon gar nicht mehr unterscheiden könne. Zu diesem mannhaften Entschluß habe ich dem gewissenhaften Forscher meinen unbedingten Beifall ausgesprochen; nur Erfahrung verschafft unumstößliche Gewißheit.
Aufgabe 10. Die Dame ist die Mutter des Herrn. Diese Aufgabe ist überhaupt nicht rechnerischer Natur, sondern erfordert lediglich die logische Vergegenwärtigung des nach den Bedingungen der Aufgabe allein möglichen Verwandtschaftsverhältnisses, das aber zumeist immer erst nach längerem Raten richtig festgestellt wird. Zumeist kommt die Mutter in den Verdacht, die Tante des jungen Mannes zu sein.
Aufgabe 11. Eine ganze Reihe von Lösern wird – zunächst wenigstens – den Personenbestand der Kompanie mit 160, andere mit 176 oder auch 177 errechnet haben, wenigstens sind diese Ergebnisse in Zuschriften an mich am häufigsten genannt worden. Sie sind jedoch falsch, wie folgende Rechnung erweist: Es sind 16 Vorgesetzte vorhanden (1 Hauptmann, 3 Leutnants, 12 Unteroffiziere), und da die Zahl der Untergebenen zehnmal so groß ist, so beträgt diese 160. Zu diesen gehören auch die Leutnants und die Unteroffiziere, die zwar Vorgesetzte, zugleich aber auch Untergebene, nämlich des Hauptmanns, sind, daher im Personenbestand der Kompanie nicht extra berechnet werden dürfen. Der einzige innerhalb der Kompanie, der nicht Untergebener ist, ist der Hauptmann; dieser und die 160 Untergebenen ergeben zusammen einen Bestand der Kompanie von 161 Personen.
Aufgabe 12. Die Personenzahl dieser Kompanie ist 165 (164 Untergebene und der Hauptmann). Von diesen sind 10/ 11 = 150 Mannschaften und 1/ 11 = 15 Vorgesetzte.
Aufgabe 13. Beide heimkehrenden Kompanien zusammen zählen 2 Hauptleute und 308 Untergebene. Daraus ergibt sich die Zahl aller Vorgesetzten mit 28 und die der Mannschaften (310 – 28) mit 282.
Aufgabe 14. Die einzelne Kompanie zählt zusammen 154 Untergebene und den Hauptmann, also 155 Personen. Wer diese Zahl als Lösung berechnet hat, hat dennoch falsch gerechnet, denn in dieser Aufgabe ist nicht nach der Personenzahl, sondern nach der Kopfzahl der Kompanie gefragt worden, und da der Hauptmann seine Kompanie stets zu Pferde führt, so ist in diesem Falle noch ein Pferdekopf mitzurechnen. Also zählt jede der heimkehrenden Kompanien 157 Köpfe. Als diese vier Aufgaben seinerzeit in einem Unterhaltungsblatte aufgegeben worden waren, hat nach Bekanntgabe der Lösungen damals ein erheblicher Teil der deutschen Heeresmacht, unterstützt durch ansehnliche Truppenteile der Randstaaten, gegen mich in zahlreichen Zuschriften mobil gemacht mit der Begründung, daß, wenn das Pferd des Hauptmanns mitgezählt werden solle, das auch bereits in den drei vorhergehenden Aufgaben geschehen müsse; also seien entweder die Lösungen dieser oder die Lösung der letzten Aufgabe falsch. Darauf ist abermals zu erwidern, daß in den drei vorhergehenden Aufgaben nur nach der Personenzahl gefragt wurde, ein Pferd aber ist keine »Person«, sondern nur ein Mittel der Kriegstechnik, wie etwa die Feldküche oder ein Geschütz; einen Kopf hat ein Pferd aber dennoch, und deshalb mußte dieser bei der Kopfzahl mitgerechnet werden.
Aufgabe 15. Wenn die zehn Herren im »Goldenen Löwen« ihre Absicht wirklich ausführen und bis zur letzten der möglichen Reihenfolgen ausharren wollten, so müßten sie eine Dauersitzung von nahezu sieben Jahren veranstalten, denn so lange würde es dauern, bis bei den angegebenen Bedingungen sämtliche möglichen Reihenfolgen absolviert wären. Denn die Zahl der möglichen Reihenfolgen beträgt bei zehn Personen 3 628 000, und diese Zahl Minuten ergibt den genannten stattlichen Zeitraum. Da viele Leser diesen erstaunlichen Angaben nicht ganz trauen werden, wollen wir kurz zeigen, wie das Resultat herauskommt. Zwei Personen, nennen wir sie a und b, können unzweifelhaft nur zwei Reihenfolgen bilden, nämlich die Reihen ab und ba. Kommt noch eine dritte Person c hinzu, so kann diese in jeder der genannten beiden Reihen an drei Stellen stehen, nämlich vorn, in der Mitte oder hinten, so daß jetzt 2 × 3 = 6 Reihenfolgen gebildet werden können, nämlich die 3 Reihen cab, acb, abc und ferner die 3 Reihen cba, bca, bac. Wir merken uns, daß bei 3 Personen 1 × 2 × 3 = 6 Reihen gebildet werden können. Kommt eine vierte Person hinzu, so kann diese in jeder der vorhandenen 6 Reihen 4 Stellungen einnehmen, wie leicht nachgeprüft werden kann, so daß jetzt 1 × 2 × 3 × 4 = 24 Reihenfolgen gebildet werden können. Fahren wir in dieser Weise fort, so finden wir, daß von 10 Personen 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 verschiedene Reihenfolgen gebildet werden können, und dieses lange Produkt ergibt die obengenannte große Zahl, wie man leicht nachrechnen kann. Wir bemerken noch, daß man das Produkt aller Zahlen von 1 an bis zu einer Zahl n als n! bezeichnet, und man liest diesen Ausdruck: » n Fakultät«. Das Produkt der Zahlen von 1 bis 10 ergibt also 10! (gelesen: »zehn Fakultät«). In dieser Weise lassen sich natürlich auch die Fakultätswerte aller weiteren Zahlen berechnen, und der Leser wird finden, daß diese Werte bald ganz gewaltig ansteigen. Leicht läßt sich dann auch ausrechnen, wieviel Reihenfolgen von 11 oder 12 oder gar 20 Personen usw. gebildet werden könnten, nämlich 11! bzw. 12! bzw. 20!. Die Fakultätswerte spielen in der Mathematik eine sehr große Rolle.
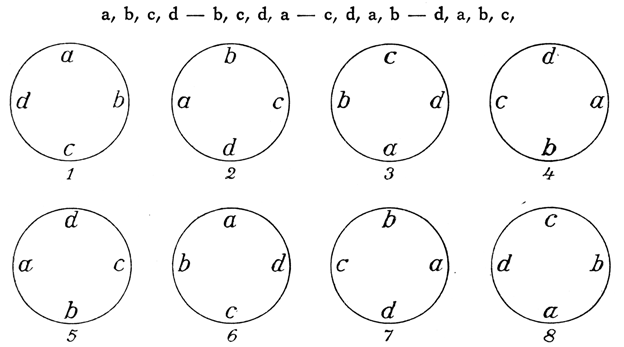
Abb. 21
Gegen die Lösung dieser Aufgabe wurde wiederholt der Einwand erhoben, daß diese nur dann zutreffe, wenn die zehn Personen in gerader Linie nebeneinander sitzen, nicht aber, wenn sie, wie es die Aufgabe vorsieht, um einen runden Tisch gruppiert sind. Durch diesen Umstand, so schrieb mir einst ein Schul- und Oberregierungsrat vom Rhein, wird die Zahl der Reihenfolgen doch erheblich eingeschränkt. Denn es sind, um ein Beispiel anzuführen, in einer Gesellschaft von 4 Herren, wenn diese als a, b, c, d bezeichnet werden, die vier Folgen
a, b, c, d – b, c, d, a – c, d, a, b – d, a, b, c,
für einen runden Tisch offenbar die gleichen, weil hierbei in allen vier Folgen jeder der vier Teilnehmer immer zwischen denselben Nachbarn sitzt. Aber auch die Umkehrungen,
d, c, b, a – a, d, c, b – b, a, d, c – c, b, a, d,
führen nicht zu anderen Folgen, auch hier sitzt wieder jeder zwischen denselben Nachbarn wie bei den ersten Folgen. Das wird anschaulich, wenn wir die genannten acht Folgen bildlich darstellen, wie es in Abbildung 21 geschieht. In allen 8 Folgen sitzt jeder Teilnehmer zwischen denselben Nachbarn. Je 8 Kombinationen führen also nach der Auffassung des Genannten immer zu derselben Folge, so daß bei 4 verschiedenen Personen an einem runden Tisch in Wirklichkeit nur 3 verschiedene Reihenfolgen möglich sind. Entsprechend wären nach seiner Auffassung in einer Gesellschaft von 5 Personen an einem runden Tisch nur 12 verschiedene Reihenfolgen möglich, und für 10 Personen rechnet er unter derselben Bedingung nur 3024 Reihenfolgen aus. Aber dieser Rechnung kann doch nicht zugestimmt werden. Zwar sitzt in den 8 Folgen unserer Abbildung 21 jedesmal jeder zwischen denselben Nachbarn, aber nicht auf denselben Plätzen bzw. denselben Stühlen. Nehmen wir an, daß auf dem Platz, den in der 1. Sitzfolge unserer Abbildung der Teilnehmer a einnimmt, das Präsidium des Tisches ist, so zeigt die Abbildung ohne weiteres, daß bei jeder der Folgen 1 bis 4 ein anderer der Herren das Präsidium innehat und jeder jedesmal auf einem anderen Stuhl sitzt. In den Folgen 5 bis 8 wiederholen sich zwar die Folgen 1 bis 4, aber nun in umgekehrter Richtung. Zwar sitzt auch jetzt wieder jeder zwischen denselben Nachbarn wie in den Folgen 1 bis 4, aber der rechte Nachbar von vordem ist jetzt sein linker und der linke von vordem jetzt sein rechter Nachbar geworden. Dieselbe Reihenfolge, bei der jeder der Teilnehmer auf demselben Platze bzw. demselben Stuhl sitzt wie in der ersten Folge, kehrt erst nach 24- bzw. 4!-maligem Platzwechsel wieder, und Entsprechendes gilt natürlich auch von einer Runde von 10 Teilnehmern, bei der erst nach 101 Änderungen der Reihenfolge die erste Folge wiederkehrt, bei der jeder Teilnehmer auf demselben Stuhl wie in jener sitzt. Damit ist auch dieser sonst durchaus scharfsinnige Einwand gegen die Lösung der Aufgabe ausreichend widerlegt. Die Mathematik macht auch am runden Stammtisch keine Ausnahme.
Aufgabe 16. Die Bedingung der Aufgabe kann mit einer Mindestzahl von vier Personen erfüllt werden, und zwar ist das dann der Fall, wenn die Gesellschaft aus zwei Brüdern besteht, die zwei Schwestern geheiratet haben.
Aufgabe 17 und 18. Die größte zweiziffrige Zahl ist natürlich nicht 99, denn der Ausdruck 9 9, gelesen: »neun hoch neun«, also eine Potenz, in der sowohl die Basis als der Exponent 9 ist bzw. ein Produkt, in welchem die 9 als Faktor neunmal gesetzt ist, ist eine ungleich größere Zahl. Ebensowenig ist 999 die größte dreiziffrige Zahl, denn die ebenfalls dreiziffrigen Ausdrücke 99 9, 9 99 stellen ungeheuer viel größere Zahlenwerte dar. Von diesen beiden ist der letztgenannte der weitaus größere. Die größte Zahl jedoch, die mit drei Ziffern gebildet werden kann, ist, wie schon Gauß erwähnt, der Ausdruck 9 9 9 , also eine Potenz mit der Basis 9, deren Exponent wieder eine Potenz von 9 ist. Dieser Ausdruck stellt, ziffernmäßig berechnet, eine Zahl dar, die mit 233 beginnt und mit über 369 Millionen Ziffern zu schreiben wäre. Der Ausdruck ist ein schönes Beispiel dafür, wie durch die symbolische Schreibweise der Mathematik selbst die allergrößten Zahlenwerte vermittels einiger weniger Zeichen ausgedrückt werden können. Man könnte auf diese Weise sogar noch viel größere Zahlenwerte mit zwei bzw. drei Ziffern bilden. Denn wie wir bereits aus der Lösung der 15. Aufgabe ersehen haben, stellt im allgemeinen jede Zahl, wenn sie mit dem Fakultätszeichen versehen wird, einen vielmal größeren Wert dar, als sie selbst hat, nämlich das Produkt aller Zahlen von 1 bis zu der fraglichen Zahl. Demgemäß könnte die größte zweiziffrige Zahl mit 9 9! und die größte dreiziffrige mit 9 9 9 ! angegeben werden. Diese Zahlen sind unendlich viele Male größer als die obenerwähnten und entsprechen ganz unvorstellbar großen Zahlenwerten.
Aufgabe 19. Die kleinsten zweiziffrigen ganzen Zahlen sind nicht etwa 11, 12 usw., sondern 2/ 2, 3/ 3, 4/ 4 usw. usw. bis 9/ 9. Jeder dieser Ausdrücke = 1. Wir können diese Zahlenwerte sogar noch etwas knapper ausdrücken und den Bruchstrich ersparen, nämlich in der Form 2 0, 3 0, 4 0 usw. Diese Ausdrücke entsprechen an Wert den genannten Brüchen, und jeder von ihnen ist ebenfalls = 1, da jede Potenz mit dem Exponenten 0 den Wert 1 hat. Falsch dagegen sind die mir wiederholt mitgeteilten Lösungen 1/ 2, 1/ 3, 1/ 4 usw. Diese Zahlenwerte sind zwar noch kleiner als 1, aber es sind keine ganzen Zahlen, wie es die Aufgabe erfordert.
Aufgabe 20. Es sind zunächst in dem größten Gefäß 8 Liter Milch, in jedem der anderen Gefäße 0 Liter enthalten. Durch Umgießen bekommen die drei Gefäße nacheinander die folgenden Inhalte:
| 8-Liter-Gefäß | 5-Liter-Gefäß | 3-Liter-Gefäß |
| 3 | 5 | 0 |
| 3 | 2 | 3 |
| 6 | 2 | 0 |
| 6 | 0 | 2 |
| 1 | 5 | 2 |
| 1 | 4 | 3 |
Jetzt sind in dem mittleren Gefäß 4 Liter enthalten, womit die Aufgabe gelöst ist. Die Lösung kann auch noch durch andere Umgießungen erreicht werden.
Aufgabe 21. Das Loch, das die Rechnung hat, besteht in der Behauptung des Gastes, daß er für den Kognak den Apfelkuchen »zurückgegeben«, d. h. in dem Sinne, wie er es aufgefaßt haben will, an Zahlungs Statt gegeben, habe. Das ist aber keineswegs der Fall gewesen. Er hat vielmehr, als er statt des Apfelkuchens den Kognak verlangte, nur die Annahme des Apfelkuchens verweigert und die Bestellung geändert. Er hatte also den Apfelkuchen noch nicht erhalten und konnte ihn daher auch nicht als Zahlung für etwas anderes geben. Zu dieser Aufgabe schrieb mir einst ein Fachmann, Oberkellner in einer Konditorei, daß er eine zweckdienlichere und einfachere Lösung der Aufgabe kenne: er würde einem Gast, der ihm mit einer so merkwürdigen Rechnung käme, mit einer Gegenrechnung dienen, nämlich ihm fünfe ins Gesicht dividieren; dann würde der Gast wohl wissen, was er zu bezahlen habe! Stimmt, und ist wieder ein Beweis, daß die Praxis der Wirklichkeit über Logik und Rechenkunst hinausgeht.
Aufgabe 22. Die Antwort des Herrn war natürlich logisch unrichtig. Denn er wollte doch – das war der Sinn des Witzes – durch seine Worte der Dame zu verstehen geben, daß ihre Behauptung, sie habe erst dreimal gelogen, unwahr sei. Dann mußte nach seiner Meinung die Dame also schon vor jener Bemerkung mehr als dreimal, also zum mindesten viermal, gelogen haben, und ihre Bemerkung wäre zum mindesten die fünfte Lüge gewesen. Also auch in einem Witzblatt können unfreiwillige Witze gemacht werden, und ich gestehe, daß ich mich über die Entdeckung dieses Falles viel mehr gefreut habe als über den höchst mäßigen Witz selber.
Aufgabe 23. Rauch und Asche sind zusammen nicht leichter, sondern schwerer als die Zigarre, aus der sie entstanden sind. Denn beim Verbrennen verbindet sich der Kohlenstoff in der Zigarre mit Sauerstoff aus der Luft; das Verbindungsprodukt beider ist der Rauch, der also den Kohlenstoff der Zigarre und überdies noch ein Quantum Sauerstoff enthält, das vordem nicht in der Zigarre enthalten war. Um das Gewicht des aufgenommenen Sauerstoffs müssen also die Verbrennungsprodukte, Rauch und Asche, schwerer sein als die ursprüngliche Zigarre. Die Richtigkeit dieser Aufgabe wurde nur ein einziges Mal bestritten, und zwar von einem Herrn, der mir seine Kompetenz, den Fall besser und richtiger beurteilen zu können – er behauptete, Asche und Rauch müßten ein geringeres Gewicht als die Zigarre haben –, damit nachzuweisen suchte, daß er sich mir als Realschullehrer und Verfasser eines weitverbreiteten Schulbuches für den Unterricht in Physik und Chemie legitimierte. Ich antwortete ihm: Bedauernswerte Schüler!
Aufgabe 24. Die beteiligten Personen waren Großvater, Vater und Sohn, wodurch das Ergebnis zustande kam.
Aufgabe 25. Viele Leser werden – wenigstens auf Anhieb – den Wert des Korkes mit 10 Pfennigen berechnet haben. Das ist aber falsch, denn dann würde die Flasche 1 Mark kosten und wäre nur 90 Pfennige teurer als der Kork. Der Kork kostet vielmehr 5 Pfennig, die Flasche 1,05 Mark, und damit stimmt die Rechnung. So einfach die Aufgabe ist, so verführen doch die Angaben zunächst meistens zu der angegebenen falschen Lösung. Ein Leser schrieb mir einst nach Veröffentlichung der Aufgabe eine Postkarte sehr ungehaltenen Inhaltes, ob ich die Leute denn für kleine Kinder halte, daß ich mit solchen lächerlichen Aufgaben komme. Einen Tag später aber ließ er einen längeren Brief folgen, in welchem er sich selbst mit sehr starken Ausdrücken aus der Zoologie belegte und mitteilte, daß er wieder und immer wieder herumgerechnet habe, was denn an der Aufgabe daran sei, bis ihm im Bette die Erleuchtung kam. Darauf folgten wieder längere Betrachtungen der Selbsterkenntnis mit reichlichem zoologischen Einschlag und das Versprechen, in Zukunft gerade bei den anscheinend leichten Aufgaben alle Geisteskräfte mobil zu machen.
Aufgabe 26. Der Hut kostet 10, der Stock 20 und der Mantel 110 Mark.
Aufgabe 27. Genau 2¼ Stunde, nachdem Herr Schwarz seine Wohnung verlassen hat, ist das von ihm aufgegebene Telegramm in die Hände des Mr. White in New York gelangt. Wer aber daraus den Schluß ziehen würde, daß die Uhr des Mr. White bei Empfang des Telegramms auf ¼3 bzw. ¼15 stand, hätte sich sehr geirrt. Denn die New-Yorker Zeit geht gegen die Berliner bzw. die mitteleuropäische Zeit gerade sechs Stunden nach. Die Uhr des Mr. White zeigte daher, als das Telegramm anlangte, ¼9 vormittags. Nach dem beiderseitigen Uhrenstande berechnet, hätte also Mr. White das Telegramm früher bekommen, als es abgesandt worden war.
Aufgabe 28. Der Esel trug 5, das Maultier 7 Säcke.
Aufgabe 29. Die Aufgabe stellt eine einfache Gleichung mit einer Unbekannten dar, aus der sich ergibt, daß Diophants Knabenzeit mit 14 Jahren beendet war, daß ihm mit 21 Jahren der Bart sproß, daß er mit 33 Jahren heiratete, mit 38 Jahren einen Sohn bekam und mit 84 Jahren starb, nachdem schon vier Jahre vorher sein Sohn im Alter von 42 Jahren gestorben war.
Aufgabe 30. Die vier Springbrunnen füllen vereint die Zisterne in 12/ 25 Tagen = 11 Stunden 31 Minuten 12 Sekunden.