Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

4. Der widerspenstige Winkel
(Das Trisektionsproblem)

Die Entstehung des Problems – Mögliche und unmögliche Winkelteilungen – Vermeintliche Lösungen – Die Einschiebungsmethode – Außenseiter – Die Lösung des Problems

Das dritte jener berühmten geometrischen Probleme, die sich an Zirkel und Lineal knüpfen, und deren Lösung die Wissenschaft viele Jahrhunderte hindurch nachging, ohne sie finden zu können, ist die Dreiteilung des Winkels, auch kurz Trisektionsproblem genannt. Es besteht, wie ja schon die Bezeichnung erkennen läßt, darin, eine Methode anzuwenden oder zu erfinden, durch die unterschiedslos jeder Winkel in drei Teile geteilt werden kann, und hierbei als Hilfsmittel nur Zirkel und Lineal zu benutzen.

Auch über die Eigenart dieses Problems wird uns am besten eine kurze geschichtliche Betrachtung Aufschluß geben. Auch dieses Problem war schon im Altertum bekannt und schon in der Schule der Pythagoreer aufgetaucht. Die hatten sich viel mit Kreisteilungen beschäftigt, das heißt mit der Aufgabe, die Peripherie eines Kreises auf geometrischem Wege in gleiche Teile zu teilen. Man hatte bereits die Drei-, Vier-, Fünf-, Sechs-, Zehn-, Zwölf- und Fünfzehnteilung und ähnliche Teilungen einfacher Zahlenverhältnisse gefunden, während andere Teilungen, wie etwa die Sieben-, Neun- oder Dreizehnteilung, damals auch noch die Siebzehnteilung, sich als nicht möglich erwiesen. Man ging nun weiter und suchte die genannten Teilungen auch auf einem beliebigen Stück eines Kreisbogens auszuführen, bzw. einen beliebigen Winkel (auch der Kreis ist ja nur als ein Winkel von 360 Grad aufzufassen) in ebensolcher Weise zu teilen, wie es beim ganzen Kreise möglich war. Auch für die Lösung dieser Aufgabe galten nur Zirkel und Lineal als zulässige Hilfsmittel. Während nun die Zwei- und demgemäß auch die Vier-, Acht-, Sechzehnteilung usw. eines beliebigen Winkels spielend leicht war, zeigte es sich, daß die Dreiteilung, abgesehen von bestimmten Ausnahmefällen, unüberwindliche Schwierigkeiten bereitete und sich trotz alles darangesetzten Scharfsinnes keine Methode ausfindig machen ließ, die die exakte Lösung jenes Problems bedeutet hätte, vermöge deren es also möglich gewesen wäre, jeden beliebigen Winkel in exakt mathematischer Weise in drei gleiche Teile zu teilen. Damit war ein weiteres geometrisches Rätsel gegeben, das der Quadratur des Kreises wie auch dem Delischen Problem ebenbürtig an die Seite trat und nicht weniger als diese die Ursache ungezählter scharfsinniger Bemühungen der Mathematiker wurde, Bemühungen, die die Jahrhunderte hindurch, das ganze Altertum, seit es überhaupt die exakte Mathematik entdeckt hatte, und ebenso das gesamte Mittelalter, das die Mathematik allerdings mit mehr Eifer als Erfindungsgabe betrieb, hindurch fortgesetzt wurden, aber ebenso wie bei jenen anderen geometrischen Aufgaben immer wieder ergebnislos verliefen.

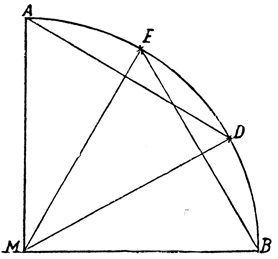
Abb. 6

Allerdings muß hier eine Einschränkung gemacht werden. Nur die Aufgabe, einen Winkel allgemein mit Zirkel und Lineal zu dreiteilen, erwies und erweist sich als unlösbar. Der Nachdruck liegt dabei auf dem Wörtchen »allgemein«, und das will besagen, daß die verlangte und gesuchte Methode der Trisektion für ausnahmslos alle Winkel in der gleichen Weise anwendbar sein soll. Sehr viele Winkel nämlich sind mit Zirkel und Lineal sehr leicht in drei Teile zu teilen. Um beispielsweise diese Operation bei einem Winkel von 90 Grad auszuführen, schlägt man um den Scheitelpunkt M des Winkel AMB, wie unsere Figur 6 zeigt, einen Kreis. Dann braucht man nur den Radius des so entstandenen Viertelkreises einmal von B und einmal von A aus auf der Peripherie abzutragen und erhält dann die Schnittpunkte E und D, durch welche die Peripherie und damit zugleich der gegebene Winkel in drei Teile geteilt ist, wie sich leicht beweisen läßt. Auf ähnliche einfache Weise läßt sich auch jeder andere Winkel, dessen Gradzahl durch neun teilbar ist, also auch der Winkel von 18, 27, 36, 45 oder auch 135, 180 usw. Grad, in exakt geometrischer Weise in drei Teile teilen, ebenso auch die Hälfte, der vierte, der achte usw. Teil eines solchen Winkels. Auch für gewisse andere Winkel ist jene Operation, wenn auch in anderer und nur sehr komplizierter Weise ausführbar; so kann beispielsweise auch ein Winkel, der durch den siebzehnten Teil des Kreisumfanges dargestellt ist, mit Zirkel und Lineal in drei Teile geteilt werden, eine Tatsache, die allerdings weder dem Altertum noch dem Mittelalter bekannt war, sondern sich erst aus der Entdeckung der Siebzehnteilung des Kreises durch den genialen Gauß ergab. Aber alle diese Fälle, so zahlreich sie auch sein mögen, sind doch nur als Spezialfälle zu betrachten, die keine allgemeine Lösung des Problems, also nicht die Möglichkeit der Dreiteilung eines jeden beliebigen Winkels, bedeuten. Für die weitaus meisten Winkel haben wir keine exakte geometrische Methode der Dreiteilung; Winkel von 10, 20, 30, 40, 50 oder, um auch höhere Grade zu nennen, von 100, 200, 300 Grad usw. sind in exakter Weise nicht in drei Teile zu teilen; nur für Winkel dieser Art bestand und besteht noch das Problem und seine Unlösbarkeit, und nur um Winkel dieser Art drehte sich der ewige Geisteskampf in Altertum und Mittelalter um die Lösung dieser merkwürdigen Aufgabe.

Oftmals freilich glaubten in diesem Geisteskampfe einzelne Geometer die exakte Lösung des Problems, also eine Methode gefunden zu haben, die bei ausnahmslos allen Winkeln die Dreiteilung in exakter Weise mit Zirkel und Lineal möglich zu machen geeignet sein sollte, und die Geschichte des Dreiteilungsproblems zeigt in dieser Hinsicht große Ähnlichkeit mit der der Quadratur des Kreises. Aber die Ähnlichkeit besteht auch darin, daß solche vermeintlichen Lösungen sich immer wieder als verfehlt erwiesen. Immer ergab die genauere Nachprüfung der Lösung, daß der glückliche Entdecker entweder einen Rechen- oder Konstruktionsfehler begangen oder unbemerkt ein unzulässiges Verfahren angewandt und also zu früh triumphiert hatte. Allerdings liegt gerade beim Trisektionsproblem die Gefahr nahe, scheinbare oder annähernde Lösungen für die wirklich exakte Lösung der Aufgabe zu halten, und dieses Mißgeschick ist selbst manchem tüchtigen Geometer widerfahren. Selbst der große Leonardo da Vinci, der ja nicht nur ein hervorragender Maler, Bildhauer und Ingenieur, sondern auch ein ausgezeichneter Mathematiker und überhaupt eins der größten Universalgenies war, die die Geschichte kennt, hat eine solche von ihm gefundene Annäherungslösung für die wirkliche Lösung der Aufgabe gehalten.

Solcher Hilfs- oder Annäherungsmethoden, die von den Mathematikern selbst zur Lösung des Problems ersonnen wurden, entstanden im Laufe der Zeiten sehr viele. Besonders durch die Verwendung von Kurven der verschiedensten Art glaubte man die Lösung doch zu erzielen. Aber so scharfsinnig, geistreich und interessant diese Methoden auch oftmals waren, so konnten sie doch niemals die exakte wissenschaftliche Lösung des Problems bedeuten. Denn die einzige Kurve, die vermittels des Zirkels ausgeführt werden kann, ist eben der Kreis, und die Kreiskurve führte, wie man sich schließlich überzeugte, nicht zur vollen Lösung des Problems. Alle anderen Kurven aber erfordern entweder andere Hilfsmittel als Zirkel und Lineal oder führen immer nur zu Annäherungswerten. Wir wollen die Gefahren des Trisektionsproblems, die darin bestehen, daß manchmal selbst der mathematisch geschulte Geist Annäherungen mit der exakten Lösung verwechseln kann, an einer sehr berühmten und schon aus dem Altertum stammenden Annäherungsmethode, der sogenannten Einschiebung, veranschaulichen. Auf unserer Abbildung 7 ist ein Winkel ABC gezeichnet, der nach dieser Methode in drei Teile geteilt werden soll. Zu diesem Zwecke fällen wir von einem beliebigen Punkte A des einen Schenkels das Lot AL auf den anderen Schenkel und ziehen ferner durch den Punkt A die Parallele zu BC, alles Operationen, die nur Zirkel und Lineal erfordern. Durch den Scheitelpunkt B legen wir dann eine Gerade, die die Parallele zu BC in dem Punkte E trifft und auf ihrem Wege, wie die Abbildung erkennen läßt, das Lot AL in dem Punkte S schneidet. Dieser Schnittpunkt S teilt die Strecke BE in zwei Strecken, nämlich die Teilstrecken BS und SE. Diese Teilstrecken ändern ihre Größe, wenn die ganze Strecke BE um den Punkt B gedreht wird, wie man sich an Hand der Abbildung leicht veranschaulichen kann. Bringe ich durch Drehen und Ausprobieren nun die Strecke BE in eine solche Lage, daß die Teilstrecke SE gerade doppelt so lang wird wie die Strecke BA (unsere Abbildung stellt annähernd diesen Fall dar), so ist der entstandene Teilwinkel EBC der dritte Teil des ganzen Winkels ABC. Der Beweis für diese Behauptung wird dem geometrischen Scharfsinn unserer Leser keine Schwierigkeiten bereiten, weshalb wir ihn übergehen können. Damit ist nun die Aufgabe schon gelöst; denn wenn ich jetzt den anderen Teilwinkel ABE halbiere, was ja mit Zirkel und Lineal leicht erfolgen kann, so ist der ganze Winkel ABC auf diese Weise in drei gleiche Teile geteilt.

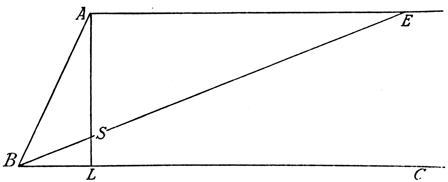
Abb. 7

Aber was hindert uns, diese Methode als exakt im wissenschaftlichen oder mathematischen Sinne anzuerkennen? Lediglich der Umstand, daß hierbei die Länge der Strecke SE, die doppelt so lang wie AB sein muß, bzw. der Punkt S, der diese Strecke bestimmt, nicht in exakter Weise durch den Schnittpunkt zweier anderer Linien, die mit Zirkel und Lineal konstruiert werden können, sondern nur durch allmähliches Ausprobieren ermittelt werden kann, was keine Gewähr für völlige Genauigkeit bietet und der Forderung mathematischer Exaktheit widerspricht. Ja, wenn sich die Lage des Punktes S auf dem Lote AL vorher mit Zirkel und Lineal bestimmen ließe, dann wäre damit das Problem der Dreiteilung des Winkels mit aller nur wünschenswerten Exaktheit gelöst, und nicht der gewissenhafteste und pedantischste zünftige Mathematiker könnte an dieser Lösung dann noch etwas auszusetzen haben. So aber bedeutet auch diese Konstruktion nur eine Annäherung, die freilich bis zu jeder gewünschten Genauigkeit durchgeführt werden kann, praktisch also vollkommen ausreicht, aber eben keine Lösung des Problems im exakt mathematischen Sinne ist.

So ging auch hier der Kampf um die Lösung des Problems bei Gelehrten und Ungelehrten weiter. Denn auch hier finden wir die Tatsache zu verzeichnen, daß das Problem außer auf die zünftigen Mathematiker auch auf die Außenseiter, die mit mathematischer Bildung mehr oder weniger unbeschwert waren, eine große Anziehungskraft ausübte, und zwar deswegen, weil die Aufgabe, rein äußerlich betrachtet, so überaus einfach und leicht erscheint. Irgendeinen Winkel mit Zirkel und Lineal in drei Teile zu teilen, das muß doch schließlich möglich sein, da doch viel schwieriger aussehende Teilungsaufgaben im Reiche der Geometrie, wie etwa die Sieben- oder Siebzehnteilung einer Strecke oder die Dreiteilung eines beliebigen Vielecks und ähnliche Aufgaben ohne weiteres lösbar sind, ohne andere Hilfsmittel als Zirkel und Lineal zu verlangen. Diese anscheinende Einfachheit und Leichtigkeit der Trisektion veranlaßte von jeher gerade auch zahlreiche Nichtmathematiker zu dem Versuch, den zünftigen Gelehrten ein Schnippchen zu schlagen und die von diesen als unmöglich bezeichnete Lösung dennoch möglich zu machen, und diese Beliebtheit hat das Problem in der Laienwelt bis auf den heutigen Tag beibehalten.

Der Jahrhunderte hindurch vergeblich um die Lösung der Aufgabe geführte Kampf wurde schließlich durch die genauere Untersuchung des Wesens des Problems beendet. Der große Gauß war es, der, wie bereits erwähnt, im Anfang des vorigen Jahrhunderts diese Untersuchung ausführte und zu dem Ergebnis gelangte, daß wie die Verdoppelung des Würfels so auch die Dreiteilung des Winkels unter der einschränkenden Platonischen Bedingung, also nur mit Zirkel und Lineal, überhaupt nicht ausgeführt werden kann, und er erbrachte den exakten Beweis für die Unmöglichkeit der Lösung dieser Aufgaben. Die Unmöglichkeit besteht wie beim Delischen Problem so auch bei der Trisektionsaufgabe darin, daß die algebraische Behandlung der Aufgabe, die ja der geometrischen Konstruktion vorangehen muß, auf algebraische Probleme führt, für die es eine Lösung nicht gibt. Auch hier führt die algebraische Behandlung der Aufgabe auf eine Gleichung dritten Grades und die geometrische Konstruktion auf die Notwendigkeit, kubische Wurzeln zu konstruieren. Weil es aber keine Methode und auch keinen Lehrsatz gibt, der, ähnlich wie der pythagoreische Lehrsatz für die Konstruktion von Quadratwurzeln, für die Konstruktion kubischer Wurzeln mit Zirkel und Lineal verwendbar wäre, so ist damit die ganze Aufgabe der Dreiteilung des Winkels als unmöglich zu bezeichnen. Allerdings liegt beim Trisektionsproblem die Sache nicht so einfach wie bei der Würfelverdoppelung. Während bei diesem die notwendigen algebraischen Operationen sehr leicht und durchsichtig sind, sind sie bei der Trisektionsaufgabe doch bereits viel schwieriger und komplizierter, und wir wollen darauf verzichten, sie an dieser Stelle durchzuführen. Aber der Grund der Unmöglichkeit ist in beiden Fällen derselbe, die Tatsache nämlich, daß die algebraische Behandlung des Problems auf eine Gleichung dritten Grades führt, deren Wurzeln mit Zirkel und Lineal nicht konstruiert werden können.

Mit dem von Gauß erbrachten Unmöglichkeitsbeweis, der mit zu den hervorragendsten Leistungen dieses unvergleichlichen Genies gehört, war das Jahrhunderte und Jahrtausende alte Ringen um die Lösung des Delischen und des Trisektionsproblems zum Abschluß gebracht werden. Das bis dahin undurchdringliche Geheimnis, das über jenen beiden Problemen lagerte, hatte sich dem forschenden Geist in seinem Wesenskern restlos enthüllt, und zwei der merkwürdigsten wissenschaftlichen Aufgaben hatten ihre Lösung gefunden. Das hat freilich nicht zu verhindern vermocht, daß jene beiden Probleme auch heute noch immer der Gegenstand ungezählter Lösungsversuche von Außenseitern sind. Zumeist ist ihnen die negative Lösung der Probleme, die die Wissenschaft mit dem Unmöglichkeitsbeweis erbracht hat, nicht bekannt, wenn ihnen diese aber bekannt wird, so wird ihre Gültigkeit mit kühner Handbewegung bestritten und ihr werden die Ergebnisse eigener Forschung entgegengesetzt. So bemühen sich also auch heute noch ungezählte Tausende, die Verdoppelung des Würfels wie auch die Dreiteilung des Winkels zuwege zu bringen. Besonders die Dreiteilungsaufgabe, die doch so leicht und mühelos anmutet und äußerlich freilich nichts von der Tiefe und Schwierigkeit dieses Problems verrät, hat noch zahllose Liebhaber, die alljährlich die Welt mit neuen Konstruktionen und Lösungen zur Bezwingung des widerspenstigen Winkels überraschen. Zu allen diesen Bemühungen aber kann nur gesagt werden, daß es heute an dem Delischen wie an dem Dreiteilungsproblem nichts mehr zu lösen gibt, denn diese Probleme sind heute, geradeso wie das der Quadratur des Kreises, als absolut erledigt zu bezeichnen, sind durch den Unmöglichkeitsbeweis endgültig entschieden. Eine andere als die von der Wissenschaft gefundene und anerkannte Lösung könnte nur darin bestehen, den Unmöglichkeitsbeweis für jene beiden Probleme zu widerlegen. Eine solche Widerlegung würde verlangen, eine Methode oder einen Lehrsatz zu finden, der in der Art des pythagoreischen Lehrsatzes die Konstruktion kubischer Wurzeln mit Zirkel und Lineal angibt. Wer also eine solche Methode oder einen solchen Lehrsatz findet, der hätte den Sieg über Plato, über Leonardo da Vinci und über Gauß davongetragen und würde mit einem Schlage zu den Unsterblichen im Reiche der Mathematik zu rechnen sein. Die Wissenschaft freilich sieht solchen Bemühungen mit Lächeln und Gemütsruhe zu; sie weiß, daß eine solche Methode unter der Bedingung Platos nicht möglich ist und hat daher endgültig Abschied genommen auch von diesen beiden Problemen, die aber, ähnlich wie der Kampf um die Quadratur des Kreises, für immer eins der eigenartigsten Kapitel in der Geschichte der mathematischen Forschung füllen.

Postskriptum

Trisektoren von heute – Beweise, die »sich erübrigen« – Der Beweis durch Abrollen – Ein scharfsinniger Jurist – Ein schwerer Fall – Ein guter Witz – Der Brief eines Toten – Die Methode der Hilfskurven – Mathematisch-finanzielle Ideen – Die Sage von dem hohen Preis – Die lockende Lorelei

Die Dreiteilung des Winkels hat es noch immer vielen angetan und zeitigt, wie bereits erwähnt, ununterbrochen eine Fülle von Lösungsversuchen mehr oder weniger sachverständiger Köpfe. Der Verfasser weiß ein Lied davon zu singen. Er hat das Dreiteilungsproblem wiederholt zum Gegenstand populärer Darstellung in Zeitungen und Zeitschriften gemacht; regelmäßig flatterten ihm nach solchen Veröffentlichungen aus nah und fern mehr oder weniger umfangreiche Ausarbeitungen zu, deren Verfasser den widerspenstigen zweischenkligen Gesellen dennoch und trotz des ablehnenden Verdiktes der Mathematiker von Fach, die mit dem Unmöglichkeitsbeweis sozusagen das Rennen um die positive Lösung dieses Problems aufgegeben haben, bezwungen zu haben und die Dreiteilung nach allen Regeln der Kunst ausführen zu können vermeinen. Die Zuschriften dieser Art sind eine überaus reichhaltige und merkwürdige Sammlung und lassen interessante Schlüsse sowohl auf die Denkungsweise wie auch auf die Psychologie ihrer Verfasser zu. Sämtliche bisher bekannten Erdteile sind in dieser Sammlung vertreten. Viele dieser Versuche lassen einen erheblichen Aufwand an Scharfsinn und Findigkeit erkennen, während andere allerdings nur höchst naiver Natur sind. »Gereizt durch den geheimnisvollen Zauber der Aufgabe habe ich mich an die Lösung der Aufgabe gemacht und glaube diese trotz Gauß im positiven Sinne gefunden zu haben –«, so schrieb mir einer dieser Problematiker, der mit diesen Worten dem Seelenzustand vieler anderer jedenfalls sehr schön Ausdruck verlieh. Unverzagtes Herangehen an den Feind, nämlich den widerspenstigen Winkel, völlige Unbeirrtheit von den Ergebnissen und der Auffassung der Wissenschaft, das ist der leicht erkennbare Charakterzug der meisten dieser Problematiker, und aus vielen ihrer Zuschriften liest man förmlich das Achselzucken darüber heraus, daß die Mathematiker die positive Lösung einer anscheinend so einfachen Aufgabe für unmöglich erklärt haben. Oftmals ist es ja tatsächlich keine ganz leichte Aufgabe, den Fehler der vorgelegten Konstruktion ausfindig zu machen, aber gefunden hat er sich schließlich in allen Fällen, womit aber noch durchaus nicht gesagt war, daß sich die Verfasser für besiegt erklärten. Ganz besonders ungläubige Thomasse halten auch trotz des ihnen nachgewiesenen Fehlers nach wie vor an der Meinung fest, daß nicht sie, sondern daß die Wissenschaft sich irre, und finden sie für diese Auffassung keine Zustimmung, so kommt es oftmals zu einem sehr geharnischten »letzten Wort«, in welchem dann auf die üblichen Formen der Höflichkeit kein besonderer Wert mehr gelegt wird. Dagegen kann man nichts machen.

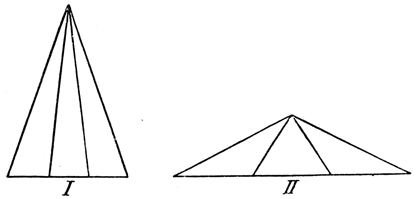
Abb. 8

Etwa die Hälfte dieser Versuche geht dem hartnäckigen Problem in der folgenden naiven Weise zu Leibe: Man schlägt um die Schenkel eines Winkels einen Kreis und verbindet die Schnittpunkte durch eine Gerade, so daß ein gleichschenkliges Dreieck entsteht; dann wird die Verbindungsstrecke auf mehr oder weniger umständliche und kunstvolle Weise in drei Teile geteilt und die Teilpunkte werden mit dem Scheitel des Winkels durch gerade Linien verbunden, die nach der Meinung dieser Konstrukteure dann auch den Winkel in drei Teile teilen. Die Figuren I und II in Abbildung 8 veranschaulichen diesen Lösungsversuch. »Der Beweis erübrigt sich«, schreiben in merkwürdiger Übereinstimmung oftmals die Einsender zu dieser Behauptung. Hierzu ist aber zu bemerken, daß sich der Beweis keinesfalls »erübrigt« und der nonchalante Verzicht auf einen solchen wohl lediglich dem Unvermögen entspringt, diesen Beweis zu erbringen. Denn die Behauptung, daß durch die Dreiteilung der Verbindungslinie auch der Winkel selbst in drei Teile geteilt wird, ist absolut irrig. Bei einem spitzen Winkel scheint es allerdings so zu sein, daß das aber nur Schein ist, ersieht man sofort, wenn man einen stumpfen Winkel in dieser Weise behandelt. Wie die Figur II deutlich erkennen läßt, ist trotz der drei gleichen Teile der Verbindungslinie der hierbei entstehende Mittelwinkel viel größer als jeder der anliegenden, und entsprechend verhält es sich auch bei jedem spitzen Winkel, wenn bei einem solchen der Größenunterschied auch nur sehr gering ist. Gleich groß werden hierbei immer nur die beiden anliegenden Winkel, die aber, wie gesagt, mit dem Mittelwinkel leider nicht übereinstimmen. Das Verfahren dieser Problemlöser ist also sehr einfach, ihre Haupttätigkeit besteht zumeist darin, die Verbindungslinie in drei Teile zu teilen. Das halten sie für das Schwierigste an dem Problem und zu diesem Zweck erfinden sie unnötigerweise die kompliziertesten Methoden, unnötigerweise deswegen, weil jede Strecke in höchst einfacher Weise mit Zirkel und Lineal nicht nur in drei, sondern in jede beliebige Zahl gleicher Teile geteilt werden kann, was schon in den Anfangsgründen der Schulgeometrie gelehrt wird. Manche dieser Forscher aus innerem Drang ließen sich durch die verblüffende Einfachheit, mit der sie die Aufgabe gelöst zu haben glaubten, in ihren Zuschriften daher zu der zarten Andeutung verleiten, daß das angebliche Problem wohl nur in meinem Kopfe spuke oder ich mir nur einen Aprilscherz erlaubt habe, »denn anders kann es einfach nicht sein«, wie mir eine Dame aus Argentinien schrieb, die auch zugleich mitteilte, daß sie das Problem »überraschend schnell gelöst und knapp in einer Nacht die Dreiteilung der Verbindungslinie herausbekommen« habe. Die Konstruktion, die dieser fundamentalen Aufgabe gewidmet war, nahm nahezu einen Quadratmeter Papier ein, bedeckt mit einem schier undurchdringlichen Netz von Linien und Kreisbogen, geradezu eine Hochleistung geometrischen Scharfsinnes; aber die Dreiteilung des Winkels war es dennoch nicht.

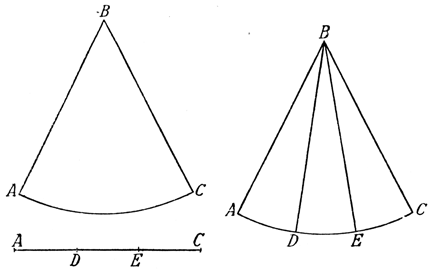
Abb. 9

Nicht ganz so einfach macht es sich eine andere Kategorie von Lösern, die sich von folgendem Gedanken leiten läßt: Man verbindet die Schenkel des Winkels durch einen Kreisbogen, verwandelt diesen dann in eine gerade Linie gleicher Länge und teilt diese in drei gleiche Teile, wie es Abbildung 9 veranschaulicht. Wird diese also geteilte Linie dann wieder in den Kreisbogen zurückverwandelt, so ist dieser und damit der Winkel selbst in drei Teile geteilt. Das wäre an und für sich auch durchaus richtig; die Dreiteilung des Kreisbogens ist tatsächlich gleichbedeutend mit der Dreiteilung des Winkels selbst und damit mit der Lösung des Problems. Aber leider stößt auch dieses so plausibel erscheinende Verfahren auf Tücken und Hindernisse. Denn ein Kreisbogen läßt sich mit Zirkel und Lineal leider auf keine Art und Weise in eine gerade Linie gleicher Länge verwandeln, denn das käme auf die Quadratur bzw. die Rektifikation des Kreises heraus, eine Aufgabe, deren Lösung mit Zirkel und Lineal genau so unmöglich ist wie die Dreiteilung des Winkels. Andere Löser dieser Gattung glauben den Kreisbogen durch »Abrollen« eines Kreissegmentes in eine gerade Linie gleicher Länge verwandeln zu können, wozu aber zu bemerken ist, daß dieses Verfahren im Sinne der Platonischen Bedingung, die nur Zirkel und Lineal zuläßt, eine unzulässige Operation ist; sonst würde es ebenfalls stimmen. Andere Löser wollen den Kreisbogen »nur mit Zirkel und Lineal« durch Ausprobieren in die nötigen drei Teile teilen, was aber an dem Umstande scheitert, daß auch dieses »Ausprobieren« keine zulässige, d. h. keine exakte geometrische, Methode ist, weil für die auf solche Weise ausprobierten Teilpunkte niemals der exakte Beweis erbracht werden kann, daß es auch wirklich die Teilpunkte im geometrischen Sinne sind, denn solche können immer nur durch Schnittpunkte von Linien, geraden oder krummen, erzeugt werden.

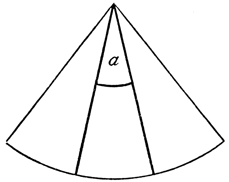
Abb. 10

Einen genialen Einfall hatte ein scharfsinniger Jurist. Er argumentierte folgendermaßen: Ich konstruiere einen beliebigen Winkel a, lege dann an jeden Schenkel dieses Winkels vom Scheitelpunkte an einen Winkel gleicher Größe (Abbildung 10), alles Operationen, die sich mit Zirkel und Lineal ausführen lassen, und erhalte auf diese Weise einen Winkel, der als der Gesamtwinkel der drei anderen in genau drei gleiche Teile geteilt ist, und zwar mit aller nur wünschenswerten mathematischen Exaktheit, selbst Plato hätte es nicht genauer machen können. Das ist absolut richtig; der auf diese Weise konstruierte Winkel besteht ganz zweifellos aus drei gleichen Teilen, und es ist keinerlei Verstoß gegen die Platonische Bedingung erfolgt. Aber leider hat auch diese geniale Konstruktion ihren Haken, denn was hierbei geschehen ist, ist nicht die Dreiteilung eines gegebenen Winkels, sondern die Aneinanderfügung dreier gleicher Winkel zu einem neuen Winkel, das heißt also die Verdreifachung oder die Multiplikation eines Winkels und damit gerade das Gegenteil der verlangten Aufgabe. Also konnte auch diesem scharfsinnigen Logiker trotz der unbestreitbaren Originalität seines Gedankens der Preis nicht zuerkannt werden. Aber einmal konnte ich einem Trisektor doch bestätigen, daß die von ihm konstruierte Dreiteilung eines Winkels als absolut richtig und korrekt zu bezeichnen sei, und zwar vollkommen unter Wahrung der Platonischen Bedingung; nur hatte er leider seinen Versuch an einem Winkel von 90 Grad unternommen, und ein solcher ist, wie überhaupt jeder Winkel, dessen Gradzahl durch 9 teilbar ist, immer in exakter Form in drei Teile zu teilen, und zwar in ganz einfacher Weise und ohne die ungeheuerlich komplizierte und verzwickte Konstruktion, die dieser Problematiker erdacht und ausgeführt hatte, um an das Ziel zu kommen. Für die Dreiteilung eines beliebigen Winkels aber reichte auch diese Konstruktion nicht aus, und so mußte auch hier eine Hoffnung getäuscht werden.

Ein Herr endlich teilte mir sein Verfahren mit, daß nicht nur die Dreiteilung, sondern sogar jede beliebige Teilung eines Winkels mit mathematischer Exaktheit möglich machen sollte. Er hatte, begeistert von seiner Idee, seine Bearbeitung sogar gleich drucken lassen; es war eine stattliche Broschüre geworden, versehen mit sehr vielen und schönen Zeichnungen und einem Vorwort, in welchem sich der Verfasser selbst begeistert als denjenigen pries, dem die Lösung des zweitausendjährigen Rätsels restlos gelungen sei. Natürlich ergab die Prüfung des Beweises auch hier Fehler, mehrere ganz dicke sogar, und mir blieb nur übrig, dem Verfasser, der die Broschüre übrigens siegesbewußt dem Buchhandel übergeben hatte, mitzuteilen, daß es zweckmäßiger gewesen wäre, mir seine Arbeit vor der Drucklegung zu unterbreiten, dann hätte er die mehrere hundert Mark betragenden Kosten der Drucklegung erspart.

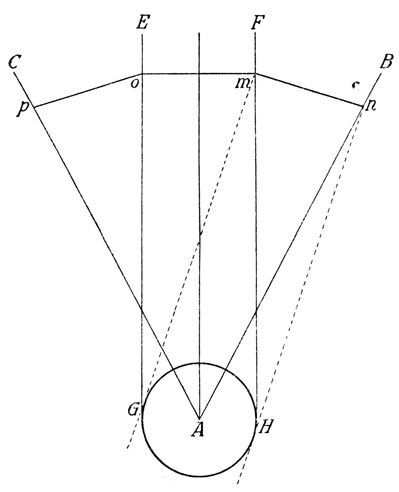
Abb. 11

Viel Vergnügen, aber auch viel Kopfschmerzen, verursachte mir die in der Abbildung 11 wiedergegebene Konstruktion zur Lösung des Problems; Vergnügen, weil es sich um eine äußerst originelle Lösung handelte, Kopfschmerzen aber deswegen, weil ich in Verlegenheit geriet, dem Urheber den Fehler klarzumachen. Der schrieb mir, daß er die Lösung des Problems endlich gefunden habe, und zwar, wie er ausdrücklich betonte, lediglich mit Zirkel und Lineal. Und dem war auch beinahe wirklich so. Zur Dreiteilung des Winkels BAC benötigt der Verfasser dieser Konstruktion eines Lineals und schlägt zunächst um den Scheitelpunkt einen Kreis, dessen Durchmesser geradeso groß wie das Lineal breit ist. Dann legt er das Lineal in der Richtung der Mittellinie des Winkels auf den Kreis und zieht die Linien EG und FH. Dann dreht er das Lineal auf dem Kreise und schiebt es dabei gleichzeitig so weit, bis die Breitseite des Lineals gleichzeitig den Schenkel BA und die Gerade FH berührt, und zieht auf der Breitseite des Lineals die Linie mn. Macht er das auf der anderen Seite des Winkels ebenso, so gewinnt er auf diese Weise die Punkte m, n, o, p. Denken wir uns dann die Punkte o und m noch mit dem Scheitel Averbunden, so ist durch diese Verbindungslinien der Winkel tatsächlich in drei Teile geteilt. Und ebenso tatsächlich sind bei der Konstruktion nur Zirkel und Lineal verwandt, unzweifelhaft eine höchst originelle Methode, der Platonischen Bedingung Genüge zu leisten. Freilich hat die Sache einen kleinen Haken. Denn der Verfasser dieser hübschen Konstruktion hat das Lineal bei der beschriebenen Operation teils als Zirkel benutzt, indem er es auf dem Kreise drehte, teils zum Einschieben der Strecke mn. Das Lineal soll aber lediglich zum Ziehen gerader Linien verwandt werden, und ein solcher weitergehender Gebrauch dieses nützlichen Instrumentes ist eine durchaus unzulässige Verwendung desselben, mit der Plato keinesfalls einverstanden sein würde. Die Einschiebung der Strecke mn in der geschilderten Weise kennzeichnet das Verfahren als Einschiebemethode nach Art der im vorhergehenden Aufsatz beschriebenen Weise. Aber das dem glücklichen Urheber dieser gescheiten Konstruktion klarzumachen, war nicht leicht, und gelungen ist es mir nicht. Auf mein diesbezügliches aufklärendes Schreiben erhielt ich eine geharnischte Antwort: Er habe, wie ich es in meinem Aufsatze als notwendig bezeichnet habe, tatsächlich nur Zirkel und Lineal bei der Konstruktion verwandt, und nun mache ich plötzlich solche Einwendungen; entweder wisse ich selbst nicht, was ich wolle, oder ich wolle ihm die Richtigkeit seiner Konstruktion aus Mißgunst nicht bestätigen. Er werde sich nunmehr an die Universitäten wenden! Da hatte ich nun mein Fett weg, und ich konnte das dem Schöpfer dieser kernigen Worte – sie waren sogar noch etwas betonter – nicht einmal übelnehmen. Mein einziger Trost war, daß, seiner Ankündigung zufolge, sich wohl noch eine ganze Reihe Universitätsmathematiker denselben Anblaser von ihm geholt haben mag.

Herzlich gelacht habe ich über die Mitteilung eines Herrn, der mir schrieb, daß ihm die Lösung des Dreiteilungsproblems restlos gelungen sei. Die Ausführung der Konstruktion erfordere gerade fünf Minuten, und er habe sie bereits einem Professor der Mathematik zur Begutachtung vorgelegt; der habe ihm aber mitgeteilt, daß fünf Minuten für den gedachten Zweck eine viel zu lange Zeit sei! Der Brave hatte nicht gemerkt, daß der Professor, der ein Mann von gutem Humor zu sein scheint, sich mit ihm einen famosen Witz gemacht hatte, denn selbstverständlich hat die Zeit mit der Richtigkeit oder Unrichtigkeit einer geometrischen Konstruktion nicht das geringste zu tun. Sogar von einem – Toten erhielt ich eine Konstruktion zur Winkeltrisektion zugesandt, allerdings nicht von ihm persönlich, denn es ist wohl anzunehmen, daß man im besseren Jenseits über solche und noch zahlreiche andere Fragen einwandfrei im klaren ist, wohl aber von seinen Hinterbliebenen. Ein Ehepaar teilte mir mit, daß der Vater eines der Gatten sich jahrelang mit dem genannten Problem befaßt und die Lösung bestimmt gefunden zu haben geglaubt hatte; kurz vor seinem Tode hatte er die Lösung in Form einer Broschüre veröffentlicht, und es war bis zu seiner letzten Stunde ein Herzensbedürfnis von ihm gewesen, dafür die Anerkennung der Nachwelt zu finden. Man bat daher um Nachprüfung der Arbeit, um gegebenenfalls dem Verstorbenen noch posthum zu der verdienten Anerkennung zu verhelfen. Die übersandte Druckschrift enthielt einen hübschen Versuch von der Art der bereits oben erwähnten Konstruktionen, bei denen die Lösung des Problems durch Rektifizierung eines Kreisbogens angestrebt wird, konnte aber aus den bereits angegebenen Gründen ebensowenig wie jene als eine wirkliche Lösung des Problems gelten. So mußte ich den Übersendern der Arbeit leider schreiben, daß es doch wohl im Interesse des Andenkens des Toten liegen dürfte, wenn die weitere Verbreitung der von ihm verfaßten Arbeit unterbliebe.

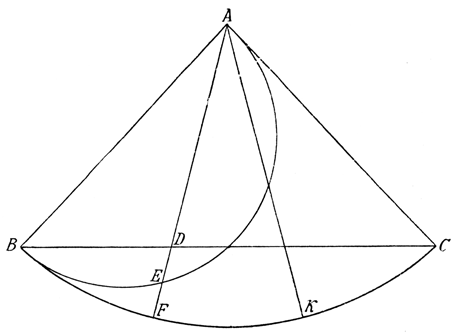
Abb. 12

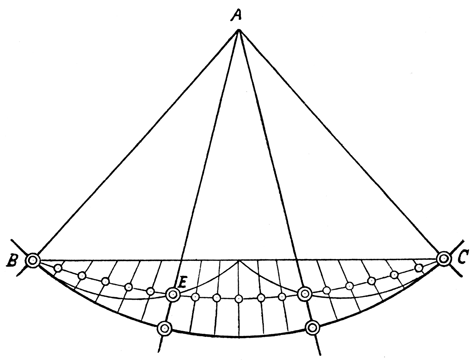
Abb. 13

Eine Anzahl der mir zugegangenen Lösungsversuche ist jedoch auch wesentlich höher einzuschätzen. Es waren das solche, die auf eine Annäherungsmethode von mehr oder weniger großer Genauigkeit hinausliefen, darunter einige, die einen bemerkenswerten Scharfsinn erkennen ließen. Einen interessanten Versuch dieser Art zeigt Abbildung 12/13. Sie wurde mir von einem mitteldeutschen Großindustriellen übersandt mit humorvoller Schilderung, daß ihm das vertrackte Dreiteilungsproblem manche schlaflose Nacht gekostet habe, bis er zur Lösung gelangt sei. Die Konstruktion ist auch noch aus anderen Gründen bemerkenswert und sei daher kurz erörtert. Angenommen, der Winkel ABC (Abbildung 12) sei durch die Strecken AF und AK in drei Teile geteilt, so schneidet der Radius AF den Halbkreis über AB im Punkte E. Zugleich halbiert der Punkt E, wie leicht zu beweisen ist, den Abschnitt DF des Radius AF. Es kommt also auf die Bestimmung des Punktes E an, durch den die eine der beiden Dreiteilungsstrecken gehen muß. Das erreichte der Einsender durch die in Abbildung 13 dargestellte, von ihm etwas stilisierte Konstruktion. Über der Strecke AB wird der Halbkreis errichtet (der hier nur bis zu der Verbindungslinie BC reicht); dieser ist der eine geometrische Ort für den zu bestimmenden Punkt. Dann werden von dem Scheitelpunkte A aus zahlreiche Radien gezogen. Die Abschnitte dieser Radien, die durch die Verbindungslinie BC und den Kreisbogen BC bestimmt werden, werden sodann halbiert und die Halbierungspunkte verbunden. Die Verbindungslinie dieser Halbierungspunkte der Radiusabschnitte ist der zweite geometrische Ort des zu bestimmenden Punktes E und stellt eine Kurve dar. Derjenige Radiusabschnitt, dessen Mittelpunkt auf den Halbkreis fällt, bestimmt den gesuchten Punkt E, und die durch diesen Punkt gezogene Gerade ist eine Dreiteilungsstrecke. In entsprechender Weise wird natürlich auch die andere Teilungsstrecke bestimmt und durch dieses Verfahren der Winkel in drei Teile geteilt. Es handelt sich also um die Konstruktion der die Mittelpunkte der Radiusabschnitte verbindenden Kurve. Diese Kurve nun ist die Achillesferse des interessanten Lösungsversuchs, denn sie kann nicht, wie es beim Kreise vermittelst des Zirkels möglich ist, in einem Zuge hergestellt bzw. als vollständige Linie gezogen werden, sondern es können immer nur einzelne Punkte der Kurve bestimmt werden, nämlich so viele, als Radien gezogen werden. Dadurch kann aber auch der Schnittpunkt der Kurve mit dem Halbkreis AB nicht genau ermittelt werden, denn die Kurve kann nur punktweise an den Halbkreis herangeführt werden, ohne daß es möglich ist, unter den unendlich vielen Punkten, die selbst in unmittelbarster Nähe des Halbkreises auf der Kurve liegen, exakt den einzigen und alleinigen Punkt E zu bestimmen, der der Schnittpunkt der Hilfskurve mit dem Halbkreis ist. Der Schnittpunkt kann bei diesem Verfahren also nur annäherungsweise ermittelt werden, und die ganze Konstruktion hat daher ebenfalls nur den Wert einer Annäherungskonstruktion. Immerhin ist sie durch die Einfachheit und Durchsichtigkeit der obwaltenden Verhältnisse ein schöner und interessanter Versuch, und das konnte ich ihrem Urheber zum Trost mitteilen, wenn ihm der erhoffte volle Preis für seine schlaflosen Nächte freilich ebenfalls nicht zuerkannt werden konnte.

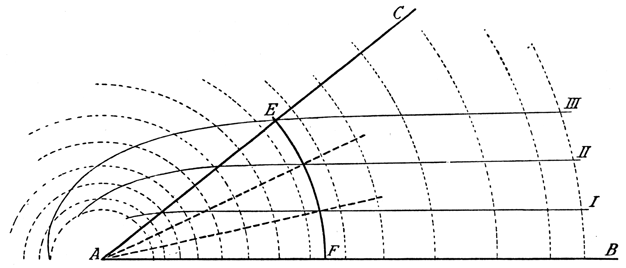
Abb. 14

Eine andere sehr hübsche und interessante Annäherungskonstruktion dieser Art ist auch die in Abbildung 14 dargestellte, die mir von Oberst v. T. übersandt wurde. Von dem Scheitelpunkt A des Winkels BAC aus werden zahlreiche Kreisbogen über dem Schenkel AB geschlagen. Auf jedem dieser Kreisbogen wird eine beliebige, aber für alle Bogen gleiche Einheitsstrecke dreimal hintereinander abgetragen. Die Verbindung dieser Teilpunkte liefert die drei Kurven I, II und III, die also auf jedem der von ihnen geschnittenen Kreisbogen drei gleiche Teile bestimmen. Ziehe ich nun durch den Punkt E, in welchem die Kurve III den Schenkel AC des gegebenen Winkels schneidet, einen Kreisbogen um A, so wird der Bogen EF und damit der durch ihn bestimmte Winkel EAF, der mit dem Winkel CAB identisch ist, durch die drei Kurven in drei Teile geteilt. Das Verfahren wirkt nahezu überraschend; tatsächlich scheint eine exakte Dreiteilung erreicht zu sein, und solche Methoden machen es erklärlich, daß manchmal selbst mathematisch geschulte Köpfe glaubten, auf diese Weise das Trisektionsproblem restlos gelöst zu haben. Aber der Mangel der Methode liegt, ähnlich wie in der vorbeschriebenen, so auch hier in dem Umstande, daß die nötigen Hilfskurven nicht vollständig, sondern immer nur punktweise konstruiert werden können und daher auch der Schnittpunkt der Kurve III mit dem Winkelschenkel AC nicht mit der nötigen mathematischen Genauigkeit bestimmt werden kann. Wohl aber ist es möglich, auf solche Weise jede gewünschte Annäherungsgenauigkeit zu erzielen.

Die vorbeschriebenen Verfahren sind typisch für die vielen Annäherungskonstruktionen, die mit Hilfskurven die Lösung geometrischer Probleme zu bewirken suchen. Was von der hier beschriebenen Kurve gesagt wurde, gilt von allen solchen Hilfskurven; sie können immer nur punktweise konstruiert werden und ermöglichen daher niemals eine wirklich exakte, sondern immer nur eine annäherungsweise genaue Ausführung der verlangten Konstruktion. In sehr vielen Fällen aber glauben die Erfinder solcher Kurvenmethoden mit diesen die Lösung des Problems wirklich gefunden zu haben, und es ist dann oftmals nicht leicht, ihnen das Zugeständnis des Mangels ihrer Methode abzuringen. Bemerkt sei noch, daß bereits die Geometer des Altertums eine ganze Anzahl solcher Hilfskurven zur Dreiteilung des Winkels erfunden hatten. Vermittels solcher Hilfskurven kann übrigens auch jede andere Winkelteilung, etwa die 5-, 7-, 9-, 11- usw. Teilung bewirkt werden. Beispielsweise brauchten in der Konstruktion der Abbildung 14 auf den einzelnen Kreisbogen nur 5 oder 7 Teile abgetragen zu werden, um auch die 5- oder 7-Teilung des Winkels zu bewirken. Ebenso kann die Methode auch dazu dienen, die Verdoppelung des Würfels und ebenso auch die Quadratur des Kreises auszuführen, selbstverständlich ebenfalls immer nur annäherungsweise. Die Methode der Hilfskurven hat bei Versuchen zur Lösung der berühmten geometrischen Probleme eine große Rolle in der Vergangenheit gespielt und spielt diese bei den heutigen Problematikern dieser Art auch noch.

Unter den Trisektoren sind übrigens nach meinen Erfahrungen in ganz besonderem Maße auch diejenigen Problematiker vertreten, die ihre kühnen Ideen zur Lösung der mathematischen Probleme zugleich mit weittragenden finanziellen Plänen verbinden. Mehr oder weniger werden ja die meisten dieser Experimentatoren den Nebengedanken hegen, wenn möglich mit ihren mühevollen Versuchen auch etwas Geld zu verdienen, was man ihnen auch wirklich nicht verargen kann. Aber bei manchen von ihnen werden diese Nebengedanken doch zu Hauptgedanken und nehmen dann die merkwürdigsten Formen an. So unterbreitete mir ein heller Sachse ein Projekt zur finanziellen Ausbeutung seiner angeblich todsicheren Lösung sowohl des Dreiteilungs- wie auch des Delischen Problems. Er schlug vor, nach Art der Rennwetten einen Totalisator für oder gegen die Richtigkeit seines Lösungsversuchs zu veranstalten, und gab der Hoffnung Ausdruck, daß sich ungezählte Tausende gern mit Einsätzen an einem solchen mathematischen Match beteiligen würden. Ferner ließe sich, wie er glaubte, auch eine erhebliche Einnahmequelle schaffen, wenn seine Lösung der genannten Probleme in Form einer Broschüre in allen Weltteilen gedruckt und über den ganzen Erdball vertrieben würde. Man sieht, Genialität und Geschäftstüchtigkeit brauchen nicht immer getrennt voneinander zu wohnen.

Gerade von dem Trisektionsproblem wird von sehr vielen Leuten angenommen, daß für seine Lösung irgendwo und von irgendwem hohe Preise ausgesetzt seien. Dazu aber ist zu bemerken, daß alle solche Erwartungen vollkommen unberechtigt sind, denn für die Lösung von Problemen, die nachgewiesenermaßen nicht gelöst werden können, werden weder von den wissenschaftlichen noch von sonstigen Instituten Preise ausgesetzt, und ob vielleicht irgendein privater Querkopf einen solchen Preis ausgesetzt hat, wie es in der Geschichte jener Probleme ja oft vorgekommen ist und übrigens bei anderen wissenschaftlichen Aufgaben auch jetzt noch vorkommt, entzieht sich meiner Kenntnis. Das Gerücht von irgendwelchen hohen Preisen für die Lösung des Dreiteilungsproblems jedenfalls erhält sich hartnäckig. So teilte mir ein Herr, der mir seine Trisektion zur Prüfung übersandt hatte, gleichzeitig folgendes mit: Er habe gehört, daß auf der Bank von England ein Preis von 50 000 Pfund für die Lösung jenes Problems deponiert sei, und habe auch dieserhalb an die Bank geschrieben; diese habe ihm jedoch mitgeteilt, daß ihr von einem solchen Depot nichts bekannt sei. Nun wolle er sich, wenn, was er mit Bestimmtheit annehme, die Prüfung die Richtigkeit seiner Lösung ergäbe, sich »behufs Erlangung eines dem Weltproblem entsprechenden Preises« an die berühmteste Universität Amerikas wenden, da bei dem verarmten Deutschland auf einen solchen Preis doch kaum zu rechnen sei. Die Richtigkeit seiner Lösung konnte ich ihm nicht bestätigen, was aber nicht ausschließt, daß er seine energischen Bemühungen um die Erlangung eines »Weltpreises« bei den Engländern oder Amerikanern fortsetzt. Es ist übrigens bemerkenswert, welche hochgespannten Erwartungen solche Problematiker für ihre Bemühungen auf das reiche Amerika setzen. Die merkwürdigsten Optimisten habe ich nach dieser Hinsicht kennengelernt. Buchstäblich wahr ist folgender Fall: Ein Herr, von Beruf Arzt und außerdem eine der bekannten problematisch-mathematischen Naturen, überbrachte mir seine Lösungen etwa eines Dutzends der berühmtesten und schwierigsten mathematischen Probleme: außer dem der Quadratur, der Dreiteilung und Würfelverdoppelung auch das des Gesetzes der Primzahlen, der Teilbarkeit der Zahlen, des Fermatschen Problems usw. Seine Überzeugung von der absoluten Richtigkeit seiner Lösungen konnten ihm auch meine Einwände nicht erschüttern, und nebenbei erzählte er mir, er wolle sich zur besseren Verwertung seiner Entdeckungen an die Amerikaner wenden; die schmissen ja für solche Dinge nur so mit den Milliarden, und er hoffe mit Bestimmtheit, auf diese Weise so viel Geld zu bekommen, um damit alle Kriegsschulden Deutschlands bezahlen zu können; das Geld werde er zu besagtem patriotischen Zweck dann Hindenburg bringen und für sich nur eine Kleinigkeit, etwa eine oder einige Millionen, behalten! Auch ich solle dann für meine Prüfung, wenn sie auch nicht zu einem mit seiner Auffassung übereinstimmenden Ergebnis gekommen sei, nicht vergessen und entsprechend honoriert werden. Ich habe keine Hoffnung darauf gesetzt, auf diese Weise zu einem ungeahnt glänzenden Honorar zu kommen, denn ich glaube, daß die kühl und nüchtern denkenden Yankees ihre Milliarden für alles andere eher als für die ausgefallenen Probleme der Mathematik anwenden werden. Solche Dinge sind nur so recht etwas für deutsche »Sinnierer«, die dauernd unerreichbaren Sphären nachstreben, wenn sie auch, wie die erwähnten Beispiele zeigen, allmählich anfangen, das Ideale mit dem finanziell Nützlichen zu verbinden, aber natürlich gleich in der unpraktischsten Weise weltentrückter Optimisten. Zur Psychologie solcher Problematiker ist dieser mammonistische Optimismus immerhin ein wertvoller Beitrag.

Das ist nur eine kleine Auslese aus der stattlichen Sammlung von Versuchen aus Laienkreisen, die Lösung eines Problems zu erzwingen, die nachgewiesenermaßen nicht möglich ist. Sie vermehrt sich noch ununterbrochen und hat manche heitere Blüte aufzuweisen. Der »geheimnisvolle Zauber des Problems« lockt wie der Sang der Lorelei und findet immer wieder seine Opfer, und das wird wohl auch noch für geraume Zeit so bleiben. Nochmals sei daher betont, daß das vielumstrittene Problem heute durch den wissenschaftlichen Unmöglichkeitsbeweis als absolut gelöst zu betrachten ist, wenn diese Lösung dem Nichtmathematiker auch nicht einleuchtet und sich ihm gefühlsmäßig die Ansicht immer wieder aufdrängt, daß eine, rein äußerlich betrachtet, so einfache Aufgabe sich dennoch in der verlangten Weise positiv lösen lasten müsse. So unmöglich es ist, aus zweimal zwei fünf zu machen, so unmöglich ist es, die Dreiteilung des Winkels mit Zirkel und Lineal auszuführen. An dieser exakt bewiesenen Unmöglichkeit müssen alle gegenteiligen Versuche scheitern. Vielleicht tragen diese Zeilen dazu bei, der so verlockenden und aufreizenden Macht, die das merkwürdige Problem noch immer auf so viele ausübt, Abbruch zu tun und die noch immer zahlreichen Problematiker dieser Art von der Vergeblichkeit ihrer Versuche zu überzeugen Unmittelbar vor Toresschluß, d. h. vor Drucklegung dieses Werkes, meldet sich noch ein Rufer im Streite um das Trisektionsproblem zum Wort. Es ist Herr De Sauerhering, der in einer Broschüre mit dem geheimnisvollen Titel »Paracaidas« sich speziell meine Wenigkeit aufs Korn nimmt und mit von keinerlei Sachkenntnis gedämpfter Energie gegen einen Aufsatz meiner Feder über die Unmöglichkeit der Winkeldreiteilung zu Felde zieht. Für Herrn De S. gibt es eine solche Unmöglichkeit nicht; er unterbreitet der staunenden Mitwelt gleich drei Methoden zur unwiderruflich richtigen Lösung des Problems und spricht mit hohem Selbstgefühl von »meiner nach 2300 Jahren erfolgten Entdeckung der, wie es Plato verlangte, nur mit Lineal und Zirkel zu vollziehenden Dreiteilung jeden Winkels«. Bedrückt widmet man sich der Lektüre der vollen 27 Druckseiten, die alle bisherigen Mathematiker in den Schatten stellen und vernichten sollen. Aber man atmet sehr bald auf. Die vorgeführten Konstruktionen und »Beweise« wimmeln von groben Fehlern, zeigen auch keinerlei Scharfsinn, der ihre Wiedergabe lohnte, sondern sind lediglich grob falsch. Ein großer Aufwand an Arbeit und Druckkosten war wiederum einmal schmählich vertan, und übrig bleibt nur ein höchst komischer Beitrag zu dem Kapitel unfreiwilligen Humors in der Mathematik..