
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Im Jahre 1908 sagte Max Planck in der Columbia-Universität zu Newyork, daß das Relativitätsprinzip an Kühnheit alles übertreffe, was bisher in der spekulativen Naturforschung, ja in der philosophischen Erkenntnistheorie geleistet wurde; die nichteuklidische Geometrie sei Kinderspiel dagegen. Aber sehr bald nachdem dies stolze Wort gefallen, und zwar von Seiten eines Physikers, der vermöge seiner ganz unbestrittenen Autorität dazu wohl die größte Kompetenz hatte, da schritt bereits Einstein zur Ausarbeitung seiner allgemeinen Relativitätstheorie, die an Kühnheit des Gedankens die bisher behandelte Relativitätstheorie um ebensoviel hinter sich ließ, wie diese die bisherige Physik.
Die bisher behandelte »spezielle Relativitätstheorie« war ohne Zweifel ein Bau, der durch seine logische Geschlossenheit und durch die Kühnheit des Gedankens imponierte; sie hatte auch durch ihre andersartige Auffassung der elementarsten Grundbegriffe, der von Raum und Zeit, bereits einen großen Einfluß auf die verschiedensten Gebiete gewonnen, aber die Möglichkeit der experimentellen Entscheidung zwischen ihr und der Lorentzschen Theorie wurde vergeblich gesucht. Sie ergab sich erst durch die allgemeine Relativitätstheorie, die sich uns als ganz natürliche Erweiterung der bisher behandelten Lehre darstellen wird. Zu ihr konnten, wie ohne weiteres klar werden wird, nur die grundsätzlich relativistischen Anschauungen Einsteins, niemals die absolutistischen von Lorentz mit ihren ad hoc ersonnenen Hypothesen hinführen. Eine Bestätigung der allgemeinen Theorie durch das Experiment kann daher auch als eine Entscheidung für Einstein und gegen Lorentz aufgefaßt werden.
Um zu verstehen, um was es sich bei ihr handelt, müssen wir uns unserer einleitenden Ausführungen erinnern. Wir sprachen dort von einem kinematischen Relativitätsprinzip, demzufolge bei Beschränkung auf bloß geometrische Betrachtungen alle Bewegungen nur »relativ«, d. h. durch Bezug auf andere, an der Bewegung nicht teilnehmende Körper wahrnehmbar und verständlich seien. Demgegenüber behaupten die physikalischen Relativitätstheorien, und zwar sowohl die mechanische, Galileische, als auch die elektromagnetische, Einsteinsche, die Relativität ausschließlich der geradlinig-gleichförmigen Bewegungen. Hingegen ist die absolute Natur aller nicht geradlinigen oder nicht gleichförmigen Bewegungen bisher nicht angetastet worden. Wir machen uns das Weitere an einem Beispiel klar.
Für die allermeisten Betrachtungen kann die Bewegung der Erde, und zwar sowohl die fortschreitende als auch die rotierende, als geradlinig-gleichförmig angenommen werden. Denn die Krümmung ist so gering, daß sie sich für kürzere Zeiten nicht bemerkbar macht. Dies ist ja auch der Grund, aus dem wir im täglichen Leben von der Drehung der Erde nichts merken, worauf ja auch schon, wie oben S. 6 erwähnt, insbesondere Galilei mit allem Nachdruck aufmerksam machte.
Nun bleiben aber doch ganz erhebliche Wirkungen übrig, die nur durch die Abweichung der Erdbewegung von der geradlinigen Bahn erklärbar sind. Wir fassen sie unter dem Namen der Zentrifugalkräfte zusammen. Jeder hat schon gesehen, wie sich anhaftende Erdteilchen von einem rotierenden Rad loslösten und nach außen flogen. Ebenso hat jeder schon den Zug in der Hand verspürt, wenn er einen Gegenstand im Kreis herumführte. Derselben Wirkung unterliegen nun auch alle Körper auf der Erde. Freilich werden sie infolge der Schwerkraft nicht einfach weggeschleudert, wohl aber wird die Schwerkraft verringert, und zwar keineswegs für alle Gegenden der Erde gleich stark, sondern am meisten am Äquator, wo ja die Geschwindigkeit infolge der Rotation am größten ist, gar nicht am Pol, wo sie ja überhaupt nicht stattfindet. Diese Verschiedenheit der Schwere auf der Erde, die allerdings außer dem eben angegebenen wichtigsten Grund auch noch andere hat, läßt sich leicht nachweisen. Beispielsweise gehen ihretwegen Pendeluhren am Äquator langsamer als in größeren nördlichen oder südlichen Breiten, während Federuhren hiervon natürlich ganz unbeeinflußt bleiben.
Von der Ablenkung einer jeden hinreichend großen nordsüdlichen oder südnördlichen Bewegung aus ihrer Bahn war auch schon oben gesprochen. Die gewaltigste Wirkung der Erdrotation aber ist die Abplattung der Erde. Da die Oberfläche unseres Planeten zum großen Teil aus Wasser besteht, das den Zentrifugalkräften nachgeben kann, so läuft dies Wasser nach dem Äquator und weicht von den Polen zurück. Wäre es möglich, die Rotation der Erde aufzuhalten, so würden ungeheure Mengen Wasser nach den Polen hinströmen, weite Teile der tropischen Meere würden ausgetrocknet, hingegen die Polarzonen überschwemmt werden, ja auch ein großer Teil der gemäßigten Zonen im Wasser versinken. Man hat ausgerechnet, daß von den ganzen Alpen nur einige höchste Spitzen, wie etwa der Montblanc als Inselhügel von 950 m, die Jungfrau als winzige, 40 m hohe Felsklippe im riesigen Meere übrigblieben. Sie wären die nördlichsten Spuren Europas Nach Martus, Astronomische Erdkunde, 3. Aufl. Dresden u. Leipzig 1904. Seite 419..
Also an Wirkungen der Erdrotation fehlt es keineswegs. Es handelt sich nur um ihre Deutung. Nach der alten, vor allem auf Galilei, Newton und Huygens beruhenden Mechanik, die auch von der speziellen Relativitätstheorie in diesem Punkte nicht erschüttert wurde, ist anzunehmen, daß alle diese Wirkungen durch die Drehung der Erde »an sich«, d. h. ohne Rücksicht auf Bezugskörper, hervorgebracht seien. Diese Physik mußte also annehmen, daß, wenn sämtliche Himmelskörper verschwänden und die Erde allein im verödeten Weltenraum zurückbliebe, jene Wirkungen trotzdem bestehen blieben. Dies ist nun der Punkt, an dem Einstein Anstoß nahm. Er sagte sich etwa: Irgendein »Vorgang«, eine Energiezufuhr oder dergleichen, ist zur Aufrechterhaltung der Rotation der Erde nicht erforderlich. Sie rotiert im leeren Weltenraum ruhig weiter; im Gegenteil sogar noch etwas ungestörter als jetzt, da die allerdings sehr geringfügigen Störungen durch den Mond usw. fortfielen. Ein relativistisch geschulter Kopf wird sich fragen: Wodurch unterscheidet sich diese Rotation relativ gegen den leeren Raum von der Rotation des leeren Weltraums gegen die Kugel? Und wären dann wohl von der Drehung des leeren Raumes auch Wirkungen auf der Kugel zu erwarten?
Durch solche Überlegungen kam Einstein dazu, zu sagen: Ich fasse auch die Rotationsbewegung nur relativ auf, nämlich relativ gegen den Fixsternhimmel. Da nun aber die Erdrotation im Gegensatz zu geradlinig-gleichförmigen Bewegungen unzweifelhaft physikalische Wirkungen hervorruft, so müssen auch diese als abhängig gedacht werden lediglich von der Relativbewegung der Erde. Das heißt: Stelle ich mir vor, daß nicht die Erde um ihre Achse relativ gegen den Fixsternhimmel rotiere, sondern umgekehrt dieser um eine durch die Erde gehende »Weltachse« gegen die Erde, wie dies ja Ptolemäus wollte, so müßten bei dem angenommenen Standpunkt, da ja die allein maßgebende Relativitätsbewegung ungeändert bleibt, auch alle Wirkungen dieselben bleiben.
Hier ist eins zu bemerken: In unserm Satz liegt unzweifelhaft eine wirkliche physikalische Hypothese, keine bloße mathematisch-philosophische Interpretation eines gegebenen Sachverhalts, wie dies bei der speziellen Relativitätstheorie gegenüber Lorentz der Fall war. Insofern ist die allgemeine Relativitätstheorie vielleicht sogar leichter verständlich als die spezielle; sie deutet nicht nur, sondern sie macht ganz konkrete Aussagen über das wirkliche Verhalten der Natur, und es ergibt sich hieraus, daß sie auch eine Nachprüfung durch das Experiment gestatten muß.
In welcher Weise wäre nun in unserm Falle eine solche Entscheidung durch Experiment möglich? Theoretisch vielleicht am einfachsten und zugleich radikalsten dadurch, daß man die Sonne, den Mond und sämtliche Sterne zerschlüge und auf die Seite schaffte. Wenn sich nach ihrer Beseitigung die obenbesprochenen Zentrifugalwirkungen auf der Erde nach wie vor zeigen, dann hat die alte absolute Theorie recht; denn dann sind diese tatsächlich durch eine absolute Bewegung hervorgerufen. Bleiben sie aber aus, dann hat die relativistische Anschauung gesiegt; denn da sich nichts an der absoluten, sondern alles vielmehr nur an der relativen Bewegung geändert hätte, die Wirkungen aber trotzdem ausgeblieben wären, so wäre die Relativitätstheorie mit ihrer Behauptung endgültig und unwiderleglich im Recht.
Nun wird jeder zugeben, daß das erwähnte Experiment seine praktischen Schwierigkeiten hätte. Wie ist nun trotzdem eine Bestätigung der Theorie möglich? Einstein schloß so: Wenn der rotierende Fixsternhimmel Zentrifugalwirkungen auf der Erde auslösen würde, so müßte das bei andern großen rotierenden Massen auch der Fall sein. Es existieren nun Versuche darüber, ob etwa die großen Schwungräder unserer Dampfmaschinen derartige Wirkungen auszuüben vermögen. Wegen der Kleinheit der in Betracht kommenden Wirkung ist es jedoch noch nicht zu einer bestimmten experimentellen Entscheidung im einen oder andern Sinn gekommen.
Die Frage nach der absoluten oder relativen Bedeutung der Rotation hatte sich schon Newton gestellt und sie experimentell zu beantworten gesucht. Er hing ein Gefäß mit Wasser an Fäden auf und versetzte es durch Drillung in Rotation. Im Anfang des Versuchs, als das Wasser die Bewegung des Gefäßes noch nicht angenommen hatte, blieb seine Oberfläche eben, trotzdem es doch relativ zum Gefäß rotierte; später aber stieg es in bekannter Weise an den Wänden hoch, wiewohl es doch zwar von uns aus gesehen rotierte, aber doch relativ zum Gefäß in Ruhe war. Newton schloß daraus, daß die Drehbewegung absolut aufzufassen sei; Ernst Machs Verdienst ist es, gezeigt zu haben, daß wenn auch das Gefäß sich nicht als geeigneter Bezugskörper herausgestellt hat, die Drehung deshalb noch nicht in einem absoluten Raum stattgefunden habe. In der Tat ist es vorläufig noch unentschieden, ob nicht Zentrifugalkräfte ausgelöst werden, wenn nicht ein Gefäß von mehreren Millimetern, sondern etwa mehreren Meilen Wandstärke oder gar das gesamte übrige Weltall gegen das Wasser zu rotieren beginnen.
Während der vorige Abschnitt eine zwar gleichförmige, aber nicht geradlinige Bewegung behandelte, besprechen wir nun einen gerade umgekehrt liegenden Fall einer zwar geradlinigen, aber nicht gleichförmigen Bewegung. Wir kehren nämlich zu der schon früher erwähnten Fahrt in einem möglichst sanft und gleichmäßig betriebenen Personenaufzug zurück. Es hat schon jeder die Erfahrung gemacht, daß von dem mittleren Teil der Fahrt aus nur etwas zu merken ist, wenn man hinaussieht, die eigene Bewegung mit andern, nicht mitbewegten Gegenständen, etwa Treppen oder andern Gebäudeteilen, vergleicht, daß man hingegen das Anfahren und Anhalten auch völlig unabhängig davon wahrnimmt. Deswegen war ja auch der Schluß der mechanischen Relativitätstheorie, daß der »gleichmäßigen« Bewegung nur relative Bedeutung zukomme, der ungleichmäßigen aber absolute, d.h. auch ohne Rücksicht auf Vergleichskörper, durchaus wohlverständlich. Auch die »spezielle« Relativitätstheorie nimmt an ihm ja keinen Anstoß. Sehen wir uns nun diese Bewegung des Abfahrens und Anhaltens etwas näher an! Bei der ersteren nimmt die Geschwindigkeit zu, bei der letzteren ab, die erstere ist, wie man sagt, »beschleunigt«, die zweite »verzögert« oder auch »negativ beschleunigt«. Aber woran wird, da ja hierfür Vergleichskörper unnötig sein sollen, diese beschleunigte oder verzögerte Bewegung als solche festgestellt und gemessen? Die Antwort wird lauten: Am Raum selbst! Und da wäre doch eben wieder der Raum als selbständiges physikalisches, »absolutes« Prinzip. Und das scheint eben unbefriedigend.
Einstein wirft daher die Frage auf: Ist denn nun diese sogenannte »beschleunigte« oder »negativ beschleunigte«, d.h. verzögerte Bewegung wirklich etwas so schlechthin Unvergleichbares, durch andere Vorgänge nicht Ersetzbares? Beobachten und ergänzen wir nur ein wenig! Würde unser Aufzug sehr viel plötzlicher anhalten, als wir es gewohnt sind, so würden wir durch das Anhalten in die Höhe geschleudert, wie man durch einen einfachen Versuch mit einem Glas Wasser jederzeit sehen kann. Wenn das Stillstehen des Aufzugs ein wenig allmählicher, aber immerhin noch weit schneller erfolgte, als es in Wirklichkeit geschieht, so wäre die Folge ein gewisses Schweben, ein momentanes Befreitsein von der Anziehungskraft der Erde, von der Schwere. Umgekehrt steht es beim Anfahren, wo die Schwere sogar noch verstärkt empfunden wird. Man sieht also zunächst für Bewegungen in vertikaler Richtung: Beschleunigte Bewegungen kommen in ihren Wirkungen auf eine Änderung der Erdschwerkraft hinaus, die je nach Art unserer Bewegung verstärkt, abgeschwächt, aufgehoben oder gar überkompensiert wird. Und um diesen Gedanken weiter zu verfolgen, fragen wir: Auf welchen Eigenschaften der Körper beruht denn die ungleichförmige Bewegung und auf welchen die Erdschwerkraft? Nun, die letztere beruht auf der »Schwere« der Körper, eine Eigenschaft, die wir diesen, etwa Gold oder Blei, in höherem, jenen, etwa Wasserstoff oder Sauerstoff in geringerem Maße zusprechen, die aber sicher ganz unbedingt als allgemeine Eigenschaft aller Körper anzusehen ist. Und von welcher Eigenschaft der Körper hängt die ungleichförmige, positiv oder negativ beschleunigte Bewegung ab? Offenbar von der Trägheit! Denn vermöge ihrer Trägheit wollen sie die geradlinig-gleichförmige Bewegung beibehalten und setzen ihrer Änderung einen bald größeren, bald kleineren Widerstand entgegen. Alles, was die ungleichförmige Bewegung als so grundverschieden von der gleichförmigen erscheinen läßt, hängt mit der Trägheit der Körper zusammen. Auch in unserm Beispiel war es die Trägheit unseres eignen Körpers, die uns die Ungleichförmigkeit der Bewegung sofort empfinden ließ. Wir werden also dazu geführt, das Verhältnis von Trägheit und Schwere zueinander zu untersuchen!
Nun wird hier vom Leser, der bisher diesen Fragen ferngestanden hat, etwas viel verlangt. Er soll zunächst den großen, grundsätzlichen Unterschied von Trägheit und Schwere sich klarmachen, um sodann den Einsteinschen Gedanken von ihrer Wesensgleichheit in sich aufzunehmen. Und doch ist beides notwendig, um sowohl die Tragweite als auch die Nichtselbstverständlichkeit dieses Gedankens zu verstehen. Nun sind allerdings Trägheit und Schwere zunächst zwei ganz verschiedene Begriffe. Von der Schwere erfahren wir fast nur als Erdschwere. Diese wirkt nur in vertikaler Richtung, in horizontaler ist sie ganz ausgeschaltet. Für die Trägheit, die den Widerstand gegen jede Bewegungsänderung bedeutet, ist die Richtung ganz gleichgültig. Wenn wir eine »schwere« Kegelkugel in schneller Bewegung aufhalten wollen, so ist es ganz gleichgültig, ob diese bergauf oder bergab oder in ebener Richtung vor sich geht, d.h. es hat mit ihrer »Schwere« nichts zu tun, sondern mit ihrer Trägheit. Wollen wir dieselbe Kugel in die Höhe heben, ohne daß es uns dabei auf die Geschwindigkeit dieser Bewegung ankommt, so haben wir hingegen nur die Schwere zu überwinden, gar nicht die Trägheit. Ganz wesentlich ist, daß die »Trägheit« einem Körper an sich zukommt, die Schwere hingegen nur in bezug auf einen ihn anziehenden Körper, also gewöhnlich die Erde. Denken wir uns auf einen andern Himmelskörper versetzt, so wäre die Schwere aller Körper völlig geändert, ihre Trägheit nicht im geringsten. Befänden wir uns etwa auf einem der zum Teil ganz winzigen kleinen Planeten, so wären wir dort ohne Zweifel imstande, einen schwerbeladenen Güterwagen oder eine Schnellzugslokomotive in die Höhe zu heben, wenngleich nur langsam. Sie hingegen anzuhalten, wenn sie, selbst mit nur mäßiger Geschwindigkeit, vorbeirollten, wäre uns ebenso unmöglich wie auf der Erde.
Wie kommt es, daß bei diesem Sachverhalt Trägheit und Schwere trotz ihrer so völlig verschiedenen Natur miteinander verwechselt werden, daß also in unserm Beispiel von der »schweren« Kegelkugel gesprochen wird, trotzdem die »träge« gemeint war? Nun, deshalb, weil die Trägheit der Schwere proportional ist, eine demnach als Maß für die andere genommen werden kann. Aus diesem Grunde ist es wohl verständlich, wenn im gewöhnlichen Leben davon gesprochen wird, daß eine »schwere« Kugel sich nicht so leicht in ihrem Lauf aufhalten lasse als eine »leichte«. Die Schwere eines Körpers wird gewöhnlich mit der Wage festgestellt und daraus ganz ohne weiteres auf seine Trägheit geschlossen. Es wäre in obigem Beispiel vielleicht korrekter, davon zu sprechen, daß eine Kugel von großer Trägheit oder auch von großer »Masse« sich nur schwer aufhalten lasse, anstatt, wie man es gewöhnlich tut, hierbei von ihrem »Gewichte« zu reden. Wir sind eben völlig daran gewöhnt, daß »Schwere« und »Trägheit« oder »Gewicht« und »Masse« durchaus Hand in Hand miteinander gehen, und verwechseln sie deshalb unbedenklich. Selbstverständlich würde dies Verhältnis auch auf andern Himmelskörpern bestehen bleiben. Selbst wenn ihre Anziehungskraft von der unserer Erde so verschieden wäre, daß unsere Kraft ausreichte, eine Lokomotive zu heben, oder umgekehrt zu schwach wäre, auch nur einen Fingerhut vom Boden zu entfernen, an der Tatsache, daß auch dort die schwereren Körper die im genau gleichen Verhältnis trägeren wären, würde dies nicht das mindeste ändern. Ein jetzt leider sehr aktuelles Beispiel möge den Sachverhalt noch weiter klären! Vor dem Kriege konnte man vielleicht glauben, daß eine deutsche Mark und ein englischer Schilling gleichwertig, identisch seien. Infolge des ständigen Schwankens unserer Valuta wissen wir jetzt leider, daß das Verhältnis des deutschen zum englischen Gelde ein sich ständig änderndes, mithin an sich ganz unbestimmtes ist. Das hindert aber nicht, daß zu einem bestimmten Zeitpunkt zwischen beiden Währungen unbedingte Proportionalität besteht. Denn wie viel oder wie wenig die Mark auch gelten möge, unter allen Umständen erhalte ich für 200, 300, 400 Mark doppelt, dreimal, viermal so viel englische Noten als für 100 Mark. So sind Trägheit und Schwere zwar an sich miteinander unvergleichbar, aber an demselben Orte besteht zwischen beiden unbedingte Proportionalität.
Eine Folge dieser Tatsache ist es bekanntlich, daß, abgesehen vom Luftwiderstand, alle Körper gleich schnell fallen. Im luftleeren Raum fallen eine Bleikugel und eine Flaumfeder genau gleich schnell. Woher kommt das? Nun, auf den schwereren Körper wird die größere Anziehungskraft ausgeübt, er würde also an sich schneller fallen. Aber der trägere Körper setzt wieder der Bewegungsänderung größeren Widerstand entgegen, würde also an sich genommen sich langsamer in Bewegung setzen. Die völlige »Proportionalität« zwischen Trägheit und Schwere hat die völlig gleiche Fallbewegung für alle Körper zur Folge. Sie bleibt also auf jedem beliebigen Himmelskörper genau bestehen.
Nun sind diese Dinge natürlich längst seit Jahrhunderten bekannt und jedem Physiker völlig geläufig. Einstein aber wirft als erster die Frage auf, ob es denn richtig sei, eine so merkwürdige und dabei so allgemeine Tatsache wie die dieser Proportionalität zwischen Trägheit und Schwere einfach bloß als Tatsache, als nackte, zufällige Tatsache hinzunehmen, oder ob man nicht versuchen solle, wenn man sie schon nicht erklären könne, sie doch wenigstens zu deuten, sie irgendwie nutzbar zu machen für das allgemeine physikalische Weltbild und mit ihm zu verankern.
Um eine höchst merkwürdige Tatsache handelt es sich allerdings. Alle andern Kräfte kommen doch den Körpern in ganz verschiedenem Maße zu! Ein elektrisch geladenes Hollundermarkkügelchen etwa entwickelt starke elektrische Kräfte, während im Verhältnis dazu sein Gewicht als ganz geringfügig zu bezeichnen ist. Würde man statt dessen eine ebenso stark geladene Bleikugel untersuchen, so wäre das Verhältnis gerade umgekehrt. Eisen und Nickel können beide magnetisch werden, aber Eisen in sehr viel höherem Grade. Auch der Wärme gegenüber verhalten sich alle Stoffe höchst verschieden. Ein Liter Wasser braucht sehr viel mehr Wärme, um auf eine bestimmte Temperatur gebracht zu werden, als ein Liter Quecksilber, während diesem wieder die sehr viel größere Masse und das entsprechend größere Gewicht zukommt. Also Verschiedenheiten, wohin wir sehen, nur gerade die allgemeinsten Eigenschaften aller Körper, Schwere und Trägheit, entsprechen sich durchaus. Das »Sichwundern« ist nach Aristoteles der Anfang aller Philosophie. Während der Laie diese so wichtige Tatsache als etwas Selbstverständliches, der Erklärung nicht Bedürftiges hinnimmt, hat sie denn auch das Interesse der Physiker schon vor Aufstellung der allgemeinen Relativitätstheorie auf sich gezogen und zu einer guten Deutung im Rahmen der speziellen Relativitätstheorie geführt.
Nun zu Einsteins »Deutung«. Er sagt: Maßgebend für die Ungleichförmigkeit der Bewegung ist die Trägheit. Eine ganz wesentliche Eigenschaft der Trägheit ist ihre Proportionalität mit der Schwere. Es entsteht die Frage, ob man nicht die Ungleichförmigkeit der Bewegung durch Schwerewirkungen ersetzen und sie dadurch ihres absoluten Charakters entkleiden kann. Wir machen uns diese noch reichlich abstrakten Sätze sofort an einem Bilde klar.
Dieses von Einstein selbst herrührende und seitdem sehr oft gebrauchte Bild ist eigentlich gar nichts anderes als unser schon mehrfach erwähnter hydraulisch oder elektrisch betriebener Personenaufzug, den wir uns jetzt nur etwas besser ausgestaltet und in etwas großartigerer Aufmachung vorstellen wollen. Wir denken uns unsern Aufzug nicht wie oben erst beschleunigt, dann mit gleichmäßiger Geschwindigkeit, dann verzögert fahrend, sondern gleichmäßig beschleunigt, so daß er sich schneller und immer schneller bewegen möge. Er fahre auch nicht auf der Erde, sondern irgendwo im freien Weltenraum, weit entfernt von allen Himmelskörpern. Über den Ursprung der Kraft, die unsern Kasten in Bewegung setzt, machen wir uns weiter keine Gedanken. Wir stellen uns etwa vor, außen am Deckel sei ein Haken angebracht, an diesem befinde sich ein genügend langes Seil, und an diesem ziehe jemand, und zwar mit gleichbleibender Kraft. Die Geschwindigkeit des Kastens nimmt auf diese Weise immer mehr zu, etwa so, wie wir es von frei fallenden Körpern gewohnt sind, deren Geschwindigkeit auch, falls sie genügend lange fortgesetzt und durch keinen Luftwiderstand gebremst wird, geradezu phantastische Werte annimmt. Um unsern Erddurchmesser zu durchfallen, würde z. B. ein frei fallender Körper noch keine halbe Stunde brauchen, zu einer einzigen Lichtsekunde allerdings einige Stunden, so daß, wie wir sehen, zu derartigen Experimenten, auch wenn sie im größten Maßstab betrieben würden, im leeren Weltenraum immer noch genügend Platz vorhanden wäre, denn die Fixsterne sind ja im allgemeinen durch Lichtjahre voneinander getrennt. Über die Richtung der Bewegung, ob nach oben, unten oder sonstwie, etwas zu sagen, hat natürlich gar keinen Sinn, derartige Richtungen gibt es ja nicht im Weltenraum.
Nun befinde sich im Innern unseres Kastens ein Physiker, der mit allen Apparaten beobachten, aber aus dem Kasten entweder gar nicht oder nur in den völlig leeren Weltenraum hinaussehen kann, jedenfalls also keinerlei Vergleichskörper zur Verfügung hat. Zu welchen Schlüssen wird der Mann kommen? Er wird bemerken, daß, wenn er Gegenstände losläßt, sie sich erst langsam, dann immer schneller in einer bestimmten Richtung bewegen, und zwar alle mit ganz derselben Beschleunigung. Sie tun dies natürlich infolge ihrer Trägheit, die sie der fortgesetzten Beschleunigung des Kastens Widerstand entgegensetzen, an ihr also nicht teilnehmen und sie also sich relativ zum Kasten bewegen läßt. Aus demselben Grunde üben sie, wenn sie durch den Kasten selbst an der Weiterbewegung verhindert werden, auf die Kastenwand einen Druck aus, der sonst im leeren Weltenraum nicht zustande kommt. Da aber die Körper immer die jeweilige Geschwindigkeit des Kastens annehmen und nur ihrer Vermehrung gegenüber Trägheit zeigen, so wird dieser Druck gegen die Unterlage nicht etwa wachsen, sondern unverändert bleiben. Auch die relative Bewegung der Körper gegen den Kasten bleibt völlig dieselbe, so oft auch die Experimente wiederholt werden mögen.
Was wird nun unser Freund im Kasten dazu sagen? Offenbar etwa folgendes: Ich habe geglaubt, mich im freien Weltenraum zu befinden, wo es kein Oben und Unten und keine Schwerkraft gibt. Ich sehe, das war ein Irrtum; ich befinde mich hier ja ganz augenscheinlich unter der Einwirkung einer Schwerkraft, in einem sogenannten »Schwerefeld« oder »Gravitationsfeld«. Denn alle Körper fallen ja nach »unten«, alle genau gleich schnell, üben einen Druck auf die Unterlage aus, ganz genau so, wie ich es gewohnt war, als ich seinerzeit auf unserer lieben alten Erde Kollegs über Experimentalphysik las. Er wird sich sofort an die Arbeit machen, um die »Beschleunigung« festzustellen, mit der die Körper fallen, die ja nach unserer Voraussetzung von der Beschleunigung abhängt, mit der sich der Kasten infolge der äußeren Krafteinwirkung bewegt; er wird so versuchen, die Größe des Gravitationsfeldes, in dem er sich wähnt, festzustellen, wird dann vielleicht Rückschlüsse über die Größe und Entfernung des Himmelskörpers machen, der es seiner Meinung nach veranlaßt. Welche Experimente er auch anstellt, er wird kein anderes Resultat erhalten, auch die Spannung des Seils, die er vielleicht beobachtet, wird er auf die »Schwere« seines Kastens, nicht auf dessen »Trägheit« zurückführen; er wird sich vielleicht auch freuen, daß durch das Seil der Kasten am Herunterfallen gehindert sei; kurz: infolge der vollkommenen Proportionalität zwischen Trägheit und Schwere ist die ganze ungleichförmige Bewegung durch ein Gravitationsfeld vollständig ersetzbar. Seinen Irrtum wird unser Kastenphysiker erst dann einsehen, wenn er Vergleichskörper hat, etwa andere Himmelskörper, »relativ« zu denen er sich beschleunigt bewegt und denen er eine beschleunigte Bewegung in einer der seinen entgegengesetzten Richtung nicht zuschreiben will.
Was wird der Physiker wahrnehmen, wenn er mitsamt seinem Kasten auf einen Himmelskörper zu, etwa auf die Erde, herunterfällt? Antwort: Gar nichts! Der Kasten hat eine beschleunigte Bewegung, alle Gegenstände in seinem Innern aber gleichfalls. Und da sie genau so schnell fallen wie der ganze Kasten, so haben sie nicht die geringste relative Bewegung zu ihm. Sie »schweben« in jedem Ort des Innern und üben keinerlei Druck auf ihre Unterlage aus, falls man hier von »Unter«lage reden will, denn ein Unterschied von »oben« und »unten« ist praktisch nicht vorhanden. Unser armer Freund, der nun einer bedenklichen Katastrophe entgegeneilt, mag sich bis dahin ruhig der Täuschung hingeben, es sei alles in bester Ordnung, und er bewege sich in vollkommen gleichförmiger Bewegung im freien Weltenraum, wo es ja auch keine Schwere und kein Oben und Unten gibt. Wir sehen also: Beschleunigte Bewegung und das Gravitationsfeld, das sie veranlaßt, heben einander in den Wirkungen gerade genau auf. Soll das Gravitationsfeld durch die beschleunigte Bewegung nicht aufgehoben, sondern ersetzt werden, also ein Gravitationsfeld angenommen werden, während nur beschleunigte Bewegung vorhanden ist, so muß diese Bewegung natürlich ebenso schnell beschleunigt sein, wie eine vom Feld veranlaßte wäre, aber die entgegengesetzte Richtung haben. Beispiele: Wir fahren in einem Eisenbahnzug, der seine Bewegung gerade anhebt. Infolge der Trägheit unseres Körpers empfinden wir diese Bewegung, denn unser Körper will noch in Ruhe bleiben, wir müssen in wiederholtem künstlichem Ruck unsern Oberkörper nach vorn bewegen, und zwar so lange, bis die Bewegung des Zugs gleichförmig geworden ist. Will der Reisende nun annehmen, er sei in Ruhe geblieben, so braucht er nur zu behaupten, es sei plötzlich ein horizontal, nämlich nach hinten wirkendes »Gravitationsfeld« entstanden, das seinen Oberkörper fortwährend nach hinten gezogen habe, das aber bald darauf, nämlich wenn in Wirklichkeit die Zugbewegung gleichförmig ist, wieder verschwunden sei. Es wird natürlich nicht behauptet, daß das plötzliche Entstehen und Verschwinden solcher horizontaler »Gravitationsfelder« physikalisch ohne weiteres möglich sei, nur um die grundsätzliche Ersetzbarkeit unserer Bewegung handelt es sich. Wir sehen wieder aus diesem Beispiel: Die Bewegung war nach vorn gerichtet, das ihr äquivalente Gravitationsfeld muß nach hinten gerichtet gedacht werden, es hätte für sich allein eine Bewegung hervorgerufen, die der tatsächlich stattgefundenen gerade entgegengesetzt gerichtet war. Ganz genau umgekehrt liegt natürlich die Sache, wenn nun der Zug, etwa durch Bremsung, immer langsamer fährt und schließlich anhält. Auch hier kann unser Reisender auf seinem Standpunkt, er sei in völliger Ruhe verblieben, bestehen bleiben, wenn er nur vorn ein Gravitationsfeld annehmen will, das, wenn es wirklich existierte, natürlich eine positive Beschleunigung des Zuges nach vorn veranlaßt hätte, während in Wirklichkeit ja eine negative Beschleunigung nach vorn, eine Verzögerung der Bewegung, stattgefunden hat. Nicht schwierig ist es, einzusehen, daß das Gravitationsfeld der Bewegung nicht nur der Richtung nach entgegengesetzt, sondern auch der Größe nach völlig gleich sein muß.
Wie kann man die Stärke eines Gravitationsfeldes messen? Offenbar nicht durch die Geschwindigkeit der Bewegung, die es veranlaßt. Denn diese wird ja unter seinem Einfluß schneller und schneller, nimmt also im Lauf der Zeit jeden Wert an. Man gibt daher die Geschwindigkeit an, die nach Verlauf einer Sekunde erreicht ist. Das ist bei der Erde rund 10 m, genauer in unsern Breiten 9,81 m. Diese Zahl charakterisiert also das Gravitationsfeld der Erde. Bei der Sonne beträgt die betreffende Zahl etwa 270 m in der Sekunde, beim Monde nur 1,66 m. Die Körper fallen also dort schneller, hier langsamer als bei uns.
Wir besprechen einen möglichen Einwand gegen unsere obige Darstellung, der in Wirklichkeit die stärkste Stütze der ganzen Theorie geworden ist. Wir kehren wieder zu unserm Physiker in seinem Kasten zurück und wollen nun annehmen, es falle von außen her ein Lichtschein, etwa von einem sehr fernen Fixstern, durch ein Fenster herein. Was wird nun zu sehen sein? Nun, wir haben eben ausführlich auseinandergesetzt, daß infolge der Bewegung des Kastens eine Aberration eintreten muß. Dies ändert nun vorläufig an der Sachlage gar nichts. Denn wenn er nun auch den Stern in anderer Richtung sieht, als ihn ein ruhender Beobachter sehen würde, er hält seine Richtung natürlich für die richtige, und zu irgendwelchen neuen Schlüssen über den Bewegungszustand kommt es nicht. Aber nun behält der Kasten ja nicht etwa seine Geschwindigkeit bei, sondern diese wird größer und größer. Nehmen wir an, daß selbst in der kurzen Zeit, die der Lichtstrahl braucht, um den Kasten zu durchqueren, seine Geschwindigkeit schon wieder merklich zugenommen habe, so wäre die Folge natürlich auch eine Zunahme der Aberration, d.h. der Strahl ändert, während er den Beobachtungskasten durchsetzt, seine Richtung, mit andern Worten: der Strahl wird dem Beobachter gekrümmt erscheinen. Nun liegt natürlich ein Einwand gegen die Auffassung des vorigen Abschnittes sehr nahe: Der beschleunigt bewegte Kasten zeigt gekrümmte Lichtstrahlen, von dem ruhig in einem Gravitationsfeld aufgehängten war dies bisher noch nicht behauptet worden, also läge hier die Möglichkeit einer Unterscheidung vor; die behauptete völlige Äquivalenz zwischen der Wirkung des Gravitationsfeldes und der der beschleunigten Bewegung wäre endgültig widerlegt. Da dies nun Einstein unerträglich schien, so stellte er die gerade umgekehrte Behauptung auf: Lichtstrahlen werden auch durch Gravitationsfelder gekrümmt, und zwar in genau demselben Maße wie durch die äquivalenten beschleunigten Bewegungen.
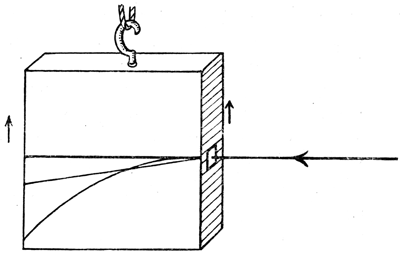
Weg des Lichtstrahls im ruhenden, gleichförmig bewegten und beschleunigten Kasten.
Diese Behauptung war deshalb so ungeheuer wichtig, weil sie die Möglichkeit zu einer ganz unmittelbaren experimentellen Nachprüfung bot. Man lasse einfach einen Lichtstrahl durch ein Gravitationsfeld hindurchgehen und sehe zu, ob es ihn gekrümmt hat. Wir wollen uns nun zunächst darüber ganz klar werden, daß starke Wirkungen nicht erwartet werden können, daß vielmehr die auf diese Weise erreichte Krümmung der Lichtstrahlen und Ablenkung aus ihrer vorigen Richtung unter allen Umständen nur ganz minimale Beträge erreichen kann. Wir wollen keine Kosten scheuen und uns unsern Kasten 300 000 km groß denken, so daß das Licht gerade eine Sekunde brauchen würde, um ihn zu durchsetzen. Mit den Dimensionen des Weltalls verglichen wäre diese Größe übrigens noch ganz winzig. Selbst von den Fixsternen der allernächsten Nachbarschaft würde man unsern Kasten, auch wenn er blendend weiß angestrichen wäre, nicht sehen können. Wir wollen ferner annehmen, es wirke auf ihn eine so ungeheure Kraft ein, daß, wenn er auch jetzt noch ruhte, er im Verlauf einer einzigen Sekunde bereits die Erdgeschwindigkeit erlangt habe, also 30 km in der Sekunde. Natürlich müßte dann diese Geschwindigkeit sich noch in jeder Sekunde um den gleichen Betrag vermehren. Unter diesen Annahmen hätte also der Lichtstrahl etwa beim Eintritt in den Kasten die Aberration Null, während sie beim Austritt diejenige Größe erlangt hätte, die der Erdgeschwindigkeit entspricht, also wie S. 39 ausgeführt ⅓ Minute oder den hundertsten Teil des Vollmond- oder Sonnendurchmessers.
Wie sieht es nun damit in der Wirklichkeit aus? Man kann sich sehr leicht davon überzeugen, daß ein derartiger Ablenkungswinkel, den wir doch längst noch nicht als sehr groß betrachten würden, nicht entfernt vorkommen kann, und zwar deshalb, weil es Gravitationsfelder von solch enormer Intensität, wie eben angenommen, in der Natur nicht gibt. Die Anziehungskraft, die die Sonne auf ihrer Oberfläche ausübt, ist etwa 28mal so groß wie die der Erde; ein Körper durchfällt bei uns im freien Fall in der ersten Sekunde etwa 4,90 m, auf der Sonne 135 m; in jeder Sekunde nimmt bei uns die Geschwindigkeit des freien Falls um 9,81 m zu, auf der Sonne um 270 m; demnach würde das Gravitationsfeld der Sonne noch nicht ganz den hundertsten Teil der Stärke haben, die wir eben voraussetzten. Und dies gilt auch nur noch für die unmittelbare Sonnenoberfläche, in der Entfernung eines Sonnenradius hat die Gravitation wiederum auf den vierten Teil abgenommen. Günstiger steht es freilich mit der räumlichen Ausdehnung des Gravitationsfeldes. Wir nahmen eben 300 000 km an; der Sonnendurchmesser beträgt aber etwa 1,4 Millionen Kilometer, also 4 bis 5 mal so viel, und das Gravitationsfeld der Sonne macht sich natürlich auf noch weitere Strecken hin, wenn auch abgeschwächt, bemerkbar.
So roh diese Überschlagsrechnung oder vielmehr Abschätzung auch ist, so zeigt sie doch zur Genüge, daß wir für unsere Ablenkung nur sehr kleine Winkel, die eben an der Grenze der Wahrnehmbarkeit stehen, zu erwarten haben werden. Ganz ausgeschlossen ist es demnach, jemals die Krümmung feststellen zu können, die ein Lichtstrahl durch den Mond erfährt, was natürlich recht bedauerlich ist, da wir zu solchen Beobachtungen oft Gelegenheit haben würden. Wir sind ganz unbedingt auf die Ablenkung durch das stärkste uns bekannte Gravitationsfeld angewiesen, und das ist das der Sonne. Wir müssen demnach einen Stern beobachten, der scheinbar ganz in der Nähe der Sonne steht, in Wirklichkeit also natürlich sehr weit hinter ihr, dessen Strahlen also, um zu uns zu gelangen, die stärksten Teile des Gravitationsfeldes der Sonne durchsetzen müssen. Nun ist aber bekannt, daß wir bei Tage, geschweige denn in so unmittelbarer Nachbarschaft der Sonne, überhaupt keine Sterne sehen können. Wenn nun ja auch die Beobachtung durch das Fernrohr in diesem Punkte sehr viel günstiger gestellt ist wie die durch das bloße Auge (denn für sie macht die Beobachtung lichtstarker Sterne bei Tage an sich keine Schwierigkeit), so kann diese Aufgabe doch nicht gelöst werden; man muß also die Gelegenheit einer totalen Sonnenfinsternis abwarten, bei der das hier hindernde, allzu grelle Sonnenlicht durch den Mond abgeblendet ist.
Nun sind die totalen Sonnenfinsternisse bekanntlich sehr selten; seit der Aufstellung der allgemeinen Relativitätstheorie haben erst zwei stattgefunden, eine im Sommer 1914, zu deren Beobachtung eine deutsche Expedition nach Südrußland entsandt wurde, die aber infolge Ausbruchs des Weltkriegs leider nicht beobachten konnte, und die vom Mai 1919, die zu der bekannten Bestätigung der Einsteinschen Vorausberechnungen geführt hat und auf die wir im folgenden zurückkommen werden.
Die Relativitätstheorie ändert, wie wir gesehen haben, unsere Vorstellung von den Raum- und Zeitmaßen. Denn während man früher diese Größen als schlechthin unveränderlich, »absolut« ansah, lehrte uns die Relativitätstheorie, und zwar schon die »spezielle«, sie als abhängig von der Geschwindigkeit, als »relativ« aufzufassen. Nun sind aber Raum- und Zeitgrößen ganz elementare Grundgrößen der Physik, die ihrerseits wieder die Voraussetzung für sehr viele andere Größen bilden. Ganz besonders gilt dies für ein Gebiet, nämlich die Mechanik. Geradezu grundlegend für diese Disziplin ist z. B. der Begriff der »Geschwindigkeit«. Man versteht darunter den Weg, der in der Zeiteinheit zurückgelegt wird; ändern sich nun infolge der Relativitätstheorie die Maßzahlen für Weg und Zeit, so wird sich auch die Maßzahl für die Geschwindigkeit ändern, und diese Änderung hat natürlich wieder die anderer, für die Mechanik nicht minder fundamentaler Größen zur Folge. Kurz, die gesamte Mechanik wird von der Relativitätstheorie in Mitleidenschaft gezogen werden, und man spricht demnach von einer »relativistischen« Mechanik, der man die ältere Theorie als die sogenannte »klassische Mechanik« gegenüberstellt.
Wie steht es nun mit den praktischen Änderungen, die unsere Neuerungen im Gefolge haben? Wir wissen, daß sie sich um so eher bemerkbar machen werden, je größer die Geschwindigkeiten sind, um die es sich dabei handelt. Nun sind die größten Geschwindigkeiten bewegter Materie, die die Physik kennt, einerseits die in den Kathoden- und β-Radiumstrahlen bewegten Massenteilchen, andererseits die astronomischen. Die ersteren Bewegungen sind zwar außerordentlich viel schneller als die letzteren, aber sie können nicht durch unmittelbare Messung festgestellt werden, sondern sie ergeben sich erst mittelbar aus der Theorie. Die Bestätigungen, die sich auf diesem Wege für die Relativitätstheorie ergeben, können zwar auch, besonders wenn sie sich häufen, ein gewisses Gewicht erlangen, aber sie lassen doch den Wunsch nach einer unmittelbaren, sozusagen handgreiflichen Prüfung der Relativitätstheorie offen, und diese kann also nur von der Astronomie geliefert werden.
Wir müssen nun hier etwas weiter ausholen. Die Astronomie lehrt zwei Bewegungen unterscheiden, die tägliche Drehung des Fixsternhimmels und die langsameren Umläufe der sogenannten Wandelsterne auf ihm. Die erstere, die sich täglich mit absoluter Präzision wiederholt, bot zu einem mathematischen Ansatz nur wenig Veranlassung und ist auch durch die von Kopernikus gelehrte Drehung der Erde um ihre Achse genügend erklärt. Hingegen stellten die Bewegungen der Wandelsterne von alters her dem Forscher zwei Aufgaben, nämlich erstens, sie genügend zu beschreiben, womöglich so, daß der Ort eines jeden Wandelsternes zu jeder beliebigen Zeit mit jeder beliebigen Genauigkeit berechnet werden konnte, und zweitens, Gründe für sie anzugeben, sie auf anerkannte Bewegungsgesetze zurückzuführen, mit andern Worten: eine Himmelsmechanik zu schaffen. Die erste Aufgabe wurde zuerst von Kepler genügend gelöst; das wichtigste der von ihm aufgestellten Gesetze besagt bekanntlich, daß die Planeten sich in ebenen Ellipsen bewegen, in deren einem Brennpunkt die Sonne steht; und auch den Zeitpunkt, in dem jeder Bahnpunkt erreicht wird, lehrte Kepler in einem zweiten Gesetz berechnen. So erstaunlich diese Leistung eines einzelnen Mannes war, die für die Sternkunde wohl ebensoviel bedeutete wie die Gesamtarbeit von anderthalb Jahrtausenden vor ihm, so ließ sie doch noch zwei Fragen offen. Erstens zeigen die sämtlichen Planetenbewegungen kleine Abweichungen von den Keplerschen Gesetzen, sogenannte »Störungen«, die zum Teil schon Kepler selbst bekannt waren, sich aber noch weit mehr bemerkbar machten, als durch die Einführung des Fernrohrs in die Astronomie die Beobachtungsgenauigkeit ganz außerordentlich gesteigert wurde. Zweitens gab Kepler seine Gesetze nur als Tatsache, eine theoretische Ableitung aus einem höheren und allgemeineren Gesetze ließ er noch vermissen.
Beide Lücken wurden in einer geradezu unerhörten Vollkommenheit ausgefüllt durch die Leistung Newtons. Er führt alle Planetenbewegungen auf zwei ganz große Prinzipien zurück, eben die in unserm Abschnitt 10 besprochenen der Trägheit und der Schwere. Nur der Trägheit folgend würden die Planeten sich in geradlinigen Bahnen immer weiter von der Sonne entfernen, nur der Schwere, der Gravitation folgend würden sie in die Sonne hineinstürzen; das gleichzeitige Wirken, das rhythmische Wechselspiel der beiden fundamentalen Prinzipien ergibt, wie Newton mit selbsterfundenen Rechenmethoden zeigte, genau die Keplerschen Bahnen. Und die Abweichungen, die sogenannten »Störungen«, ergeben sich nicht weniger vollkommen aus dem Umstand, daß ja nicht die Sonne und der betrachtete Planet allein vorhanden sind, sondern auch noch Nachbarplaneten, die auch ihrerseits Gravitationswirkungen auf ihren Bruder ausüben. Von diesen Störungen wollen wir besonders eine erwähnen: Denkt man sich den der Sonne nächsten und den von ihr entferntesten Punkt einer Planetenbahn mit der Sonne durch eine gerade Linie verbunden, so erhält man die große Achse der Ellipse, die man hier »Apsidenachse« nennt. Diese Apsidenachsen nun bleiben nicht fest im Raume stehen, sondern führen eine sehr langsame Drehung aus, derzufolge sich die Lage der Bahnellipse im Raum allmählich ändert. Da man den der Sonne am nächsten gelegenen Punkt einer Planetenbahn sein »Perihel« nennt, so spricht man auch von einer »Periheldrehung«.
Die Leistungen des Newtonschen Gesetzes grenzen nun tatsächlich ans Fabelhafte. Es wurde zum Eckstein der Astronomie, ja diese Wissenschaft wurde zum allergrößten Teil das bloße Anwendungsgebiet dieses einzigen Satzes, und dabei läßt die Astronomie, wie allseitig zugegeben wird, an Vollkommenheit alle andern Naturwissenschaften hinter sich zurück. Millionen Beobachtungen wurden durch dies Gesetz jahrelang vorher mit unerhörter Genauigkeit im voraus berechnet und hinterher von allen Sternwarten der Erde bestätigt. Seine bekannteste Leistung ist die Auffindung des Planeten Neptun, dessen Existenz und Ort aus ihm allein durch die auf den Nachbarplanet Uranus ausgeübten Störungen von Leverrier errechnet wurden. Die Wiederauffindung des zwar schon vorher entdeckten, aber in den Strahlen der Sonne verlorengegangenen kleinen Planeten Ceres durch Gauß ist eine kaum geringere Leistung. So wurde das Newtonsche Gesetz mehr und mehr das Musterbeispiel eines Naturgesetzes, und wenn je etwa ein Forscher an der Leistungsfähigkeit unserer Naturwissenschaft, an der Erforschbarkeit der Natur überhaupt verzagen wollte, so genügte ein Hinweis auf dies Gesetz, um jeden Zweifel niederzuschlagen. Anderthalb Jahrhunderte lang, bis zur Aufstellung des Gesetzes von der Erhaltung der Energie, hatte die Naturwissenschaft nichts ihm Ebenbürtiges an die Seite zu stellen.
Trotzdem hatte auch das Newtonsche Gesetz seine Mängel, theoretische und praktische. Praktische insofern, als sich doch, wenn auch außerordentlich selten und in sehr winzigem Ausmaß, Beobachtungen zeigten, die es nicht recht zu erklären vermochte; theoretische insofern, als es in der immer mehr vervollkommneten und zugleich überall in Fluß geratenen Physik als eine Art großartiger Petrefakt aus alten Zeiten stehen geblieben war. Es gestattete keine Ableitung aus einem höheren Prinzip. Es stand ferner auf dem Standpunkt der Fernwirkung, d. h. es behauptete die zeitlose Übertragung von Kräften in beliebige Fernen ohne irgendwelche Berücksichtigung des Zwischenraums, während in andern Gebieten der Physik, insbesondere seit Faraday, gerade die Leugnung solcher Fernkräfte zu den schönsten Erfolgen geführt hatte. Dazu kommt, daß es einen absoluten Raum und eine absolute Zeit voraussetzt.
Bei den eminenten Leistungen des Gesetzes war die Stellung der Physiker demgegenüber recht schwierig. Trat im weiten Gebiet der Astronomie eine Unstimmigkeit auf, so suchte man so lange nach irgendwelchen Nebenumständen, bis die Harmonie zwischen der theoretischen Forderung und der Beobachtung wieder ausgeglichen war. In den meisten Fällen gelang dies auch vollkommen; die erwähnte Entdeckung des Neptun ist ja das beste Beispiel hierfür. Sehr viel Kopfzerbrechen machte die sogenannte Mondbeschleunigung, nach der unser Trabant nach einem ganzen Jahrhundert etwa 10 Sekunden eher, als er sollte, an den errechneten Örtern erschien, und die nun gleichfalls ziemlich befriedigend erklärt ist. So blieb an ungelösten Widersprüchen eigentlich nur einer: Die Periheldrehung des Merkur ist, wie Leverrier berechnete, um 43 Sekunden im Jahrhundert größer, als sich durch Rechnung aus der Newtonschen Theorie ergibt. Um eine Vorstellung von diesem Winkel zu geben: er ist etwa gleich der scheinbaren Größe eines Millimeters in 5 m Entfernung. Auf diesen Betrag wächst also die Differenz zwischen Theorie und Praxis in einem Jahrhundert an. Man versuchte zunächst die beim Neptun bewährte Methode, man suchte nach einem neuen Planeten, dessen Gravitationswirkungen die beobachtete »Störung« ergeben hätten. Da er der Sonne noch näher stehen müßte als Merkur, der auch schon wegen seiner Sonnennähe sehr schwer sichtbar ist, so wäre es wohl möglich gewesen, daß er bisher übersehen worden wäre. Doch wollte die Entdeckung des Planeten, für den man übrigens schon den Namen »Vulkan« bereithielt, nicht gelingen.
Das Verfahren Einsteins, das alle seine Leistungen krönen sollte, können wir hier nur in groben Umrissen schildern. Er suchte nicht etwa am Newtonschen Gesetz im einzelnen herumzuflicken, sondern ging ganz selbständig neue Wege. Er verfuhr dabei deduktiv, d. h. er stellte allgemeine Grundsätze auf, die unter allen Umständen gewahrt bleiben sollten, und suchte von hier aus sein Gesetz zu gewinnen. Der erste dieser Grundsätze war der einer vollständigen Relativität. Nicht nur geradlinig-gleichförmige, sondern schlechthin alle Bewegungen sollten nur relativ aufgefaßt werden. Auf diese Weise wurde geradezu das kinematische (phoronomische) Relativitätsprinzip, das wir eingangs besprachen, und das sowohl von der mechanischen als auch von der Einsteinschen speziellen Relativitätstheorie verlassen worden war, für die Physik zurückerobert Natürlich darf man deswegen noch nicht von einer »Verwechslung« des Phoronomischen und des Dynamischen bei Einstein reden, wie dies Lenore Kipke-Kühn in ihrer etwas anspruchsvoll auftretenden Schrift: Kant contra Einstein (Erfurt 1920) tut. Ein solcher Vorwurf wäre nur dann verständlich, wenn Einstein keinen Versuch gemacht hätte, Bewegungsgesetze aufzustellen, deren Existenz gerade den Unterschied des Phoronomischen und Dynamischen ausmacht.. Das wesentlichste Mittel, durch das dies gelang, war die innere Inbeziehungsetzung von Trägheit und Schwere, die ja von uns ausführlich besprochen wurde. Es wurden sozusagen beide fundamentalen Tatsachen der Mechanik nur noch als eine einzige gewertet. Er verließ ferner grundsätzlich den Standpunkt der »Fernwirkung«, indem er sich fragte: Welche Wirkung übt ein gegebener Zustand auf seine unmittelbare räumliche und zeitliche Nachbarschaft aus? Außerdem machte er noch gewisse formal-mathematische Annahmen. Und von dieser Grundlage auf rein mathematischem Wege fortschreitend, gelang es ihm tatsächlich, ein neues Grundgesetz der Mechanik aufzustellen. Diese schon bei der speziellen Relativitätstheorie angewandte Methode, aus ganz allgemeinen, man möchte fast sagen philosophischen Grundsätzen heraus die Gesetze auszurechnen, hat für den Mathematiker etwas geradezu Faszinierendes. Über die ungeheuren dabei zu überwindenden Schwierigkeiten brauchen wir kein weiteres Wort zu verlieren. Freilich mit den üblichen Raum- und Zeitmaßen mußte Einstein dabei noch weit rücksichtsloser umgehen, als dies bei der speziellen Relativitätstheorie der Fall war. Andernfalls hätten sich eben die obenerwähnten allgemeinen Grundsätze nicht durchführen lassen. Der ganze Einsteinsche Raum erhält, in bildlichem Sinn gesprochen, dem gewöhnlichen Raum gegenüber etwas Verbogenes und Verzerrtes. Hierfür geben die obenerwähnten gekrümmten Lichtstrahlen ein gutes Bild. Sie schützen uns auch vor übertriebenen Befürchtungen! Trotzdem wir dort ein Gravitationsfeld annahmen, das hundertmal stärker war als das stärkste uns bekannte, nämlich das der Sonne, so zeigten unsere Strahlen doch selbst auf 300 000 km nur eine Krümmung von 21″, was dem Winkel entspricht, unter dem 1 mm auf 10 m Entfernung erscheint. Innerhalb bürgerlicher Dimensionen also haben wir für unsern geraden Raum und unsere geraden Glieder nichts zu befürchten! Damit ist auch schon die Antwort auf eine andere Frage gegeben: Würde es, falls wirklich die kinematische Relativitätstheorie wieder erstehen soll, auch erlaubt sein, ein fahrendes Karussell als ruhend und seine ganze Umwelt als bewegt zu betrachten, ohne dabei mit augenscheinlichen Naturgesetzen in Widerstreit zu geraten? Die Antwort kann nur lauten: Es wäre schon möglich, nur müßten wir uns dann entschließen, derartig komplizierte, von Punkt zu Punkt wechselnde Raum- und Zeitmaße einzuführen, daß wir unsern guten alten Raum und die gute alte Zeit nicht mehr wiedererkennen würden und uns die Lust zu solchem Mutwillen sehr bald verginge.
Und nun zu den Leistungen des Einsteinschen Fundamentalsatzes! Da er, wie wir sahen, grundsätzlich nur die nächste Nachbarschaft berücksichtigt, so bedarf es, will man ihn für größere Gebiete anwenden, erst einer umständlichen Ausrechnung, einer sogenannten »Integration«. Der Satz entbehrt also der geschlossenen und sehr knappen Form des Newtonschen Gesetzes. Und die notwendige Ausrechnung, die »Integration« ist nicht mit völliger, absoluter mathematischer Strenge durchführbar; sie gibt für immer weitergehende Verbesserungen Raum. Wird sie nun »in erster Annäherung« durchgeführt, so ergibt sich – das Newtonsche Gesetz! Alle die vorzüglichen Bewährungen dieses merkwürdigen Satzes, von denen wir oben sprachen, kann also die Einsteinsche Theorie mit gleichem Recht für sich beanspruchen. Aber weiter: Führt man die Ausrechnung der Grundformel noch weiter durch, so erhält man gerade die Perihelbewegung. Sie tritt für alle Planeten auf, erlangt aber nur bei dem sonnennächsten, Merkur, eine beobachtbare Größe. Und diese stimmt fast ganz genau mit der von den Beobachtungen längst geforderten überein. Das sind in der Tat erstaunliche Leistungen der Einsteinschen Theorie, denen gegenüber das Opfer der alten Raum- und Zeitvorstellungen, die ja zudem schon von der speziellen Relativitätstheorie stark erschüttert waren, nicht zu hoch erscheint.
Bei den bisherigen Erörterungen des allgemeinen Relativitätsprinzips hat der Fall eines Eisenbahnunglücks eine große Rolle gespielt und zu lebhaften, manchmal sogar hitzigen Kontroversen geführt. Man hat es als geradezu absurd hingestellt, daß sich das allgemeine Relativitätsprinzip zu der Folgerung genötigt sehe, möglicherweise sei ein in voller Fahrt verunglückter Zug in Ruhe geblieben, nur die Umgebung habe sich bewegt, sei aber andererseits doch wieder bei dem Unglück heil geblieben, während im Zuge alles in Trümmer gegangen sei. Der Sachverhalt selbst ist nicht schwierig aufzuklären; er stellt sich, wenn man, was allerdings vom Standpunkt der allgemeinen Relativitätstheorie erlaubt ist, den Eisenbahnzug als ruhendes System auffassen will, etwa so dar: Der Eisenbahnzug ruht mit der Lokomotive etwa nach Osten; die ganze Gegend: Eisenbahnschienen, Landschaft, Bäume, Häuser, bewegt sich an ihm mit großer Geschwindigkeit nach Westen vorbei. Es entsteht nun ein nach Osten gerichtetes Gravitationsfeld, demgegenüber Osten wie unten, Westen wie oben wirkt. Die Gegend, die sich nunmehr dem Gravitationsfeld entgegen, also sozusagen nach oben bewegt hatte, wird jetzt in ihrer Aufwärtsbewegung gehemmt. Sowie sie ganz zum Stillstand gekommen ist, verschwindet das Gravitationsfeld wieder, Oben und Unten haben wieder ihre normale Lage und die Gegend bleibt in Ruhe. Der Eisenbahnzug wurde durch ein äußeres Hindernis, etwa einen Stein auf den Schienen, am Fallen nach Osten verhindert; die Gegenstände im Zug natürlich nicht; Menschen, Gepäckstücke usw. fielen durcheinander. Oder auch: Nur die Lokomotive wurde am Fall verhindert, die Wagen fielen über sie hinweg, denn sie wurden ja weder durch ein äußeres Hindernis noch durch ihre bisherige Aufwärtsbewegung am Fallen verhindert. Und so ging alles kurz und klein.
Nun ist nicht zu verkennen, daß diese Beweisführung, so logisch einwandfrei sie ist, doch nicht sonderlich überzeugend zu wirken vermag. Einwände kann man natürlich widerlegen, aber das Gefühl innerer Befriedigung läßt sich nicht erzwingen. Demgegenüber möchte ich zwei Gedankenreihen andeuten, die, wie ich glaube, über die noch verbliebene Schwierigkeit hinweghelfen, und von denen die erste der Denkungsart des Nichtrelativisten entgegenkommen soll.
Erstens: Jeder, der sich auch nur ein klein wenig mit Mathematik beschäftigt hat, wird wissen, daß ein mathematischer Ansatz häufig zu mehreren Lösungen führt, von denen doch nur eine unmittelbar zur Befriedigung der Aufgabe gebraucht werden kann. Durch eine Gleichung soll vielleicht eine Anzahl von Personen ausgerechnet werden, und neben einer positiven erhält man eine negative Zahl, auch wohl eine gebrochene, die hier natürlich sinnlos ist. In der analytischen Geometrie bekommt man oft sogenannte »imaginäre Wurzeln«, die einer anschaulichen, geometrischen Deutung zunächst durchaus widerstreiten, und ähnlich steht es bei vielen andern Anwendungen. In allen diesen Fällen ist es aber sehr lehrreich, sich davon zu überzeugen, daß die gelieferten Ergebnisse, wenn sie auch keine unmittelbare praktische Verwendung finden, doch der mathematischen Logik nicht entbehren. Ich habe nun noch nie gehört, daß man es einer mathematischen Methode zum Vorwurf gemacht habe, daß ihre Lösungen über das praktische Bedürfnis noch hinausreichen.
Übrigens ist auch praktische Verwendbarkeit ein sehr relativer Begriff! Wir sehen in der Mathematik durchaus das Bestreben, ihm eine weitherzige Auslegung zu geben; wir sprechen von »negativen Strecken«, »negativen Flächeninhalten« usw., Begriffe, die auch zunächst unanschaulich sind und die ganz allein aus dem Grunde eingeführt werden, daß man mit ihrer Hilfe die Ergebnisse der Ansätze zu deuten vermag.
Ähnlich steht es hier. Wir legen aus grundsätzlichen Erwägungen Wert darauf, die Naturgesetze so zu formulieren, daß sie unsere Fragen lösen, was immer wir für Voraussetzungen über Ruhe oder Bewegung machen wollen; aber ich kann es doch einem Naturgesetz nicht zum Vorwurf machen, daß es mir mehr liefert, als ich gebrauchen will. Ich bin auch nicht gezwungen, eine Vorstellung, die, noch dazu unter Annahme von allerlei Hilfshypothesen, den Naturgesetzen nicht geradezu widerstreitet, deshalb schon für Wirklichkeit zu nehmen. Ebensowenig, wie ich gezwungen bin, jemanden, der nie mit dem Strafgesetzbuch in Konflikt gekommen ist, deswegen schon für einen anständigen Menschen zu halten.
Und übrigens: Was heißt hier »wirklich«? Sobald man einen Zustand der Ruhe als Ruhe schlechthin, als »wirkliche« Ruhe auffaßt, nimmt man eben einen absoluten Raum an, und ihn entbehrlich zu machen, ist ja eben das Ziel der Relativitätstheorie.
Die zweite Gedankenreihe führt uns vielleicht noch näher an den Geist des Relativitätsprinzips heran. Will man sich die Relativität einer Bewegung klarmachen, so gelingt dies am besten, wenn man sich ein übergeordnetes System denkt, in dem der bewegte Gegenstand tatsächlich ruht. Will man sich den fahrenden Eisenbahnzug ruhend vorstellen, so denke man einfach daran, daß er ja auf der bewegten Erde fährt und mich niemand hindern kann, anzunehmen, daß seine Bewegung und die der Erde sich gerade aufheben, so daß ich tatsächlich den Eisenbahnzug mit noch höherem Rechte als die Erde als ruhend ansehen kann. Nun ist es freilich bei ungleichförmiger Bewegung schwieriger, sich ein übergeordnetes System zu denken, in dem unser Zug in jedem einzelnen Augenblicke ruht. Das Fixsternsystem kann es jedenfalls nicht sein; denn daß unser Zug nicht zu diesem dauernd in Ruhe gedacht werden kann, steht fest. Wir denken uns deshalb ein System noch über das Fixsternsystem hinaus. Wir stellen uns einen mächtigen, im übrigen physikalisch interessierten Geist vor, der mit einem kolossalen, noch über die Fixsterne hinausreichenden Lattengerüst in der Welt herumhantiert. Auf diesem Gerüst, das sonst gewichtslos gedacht ist, seien weithin sichtbar Kilometerzahlen und vielleicht auch Meterzahlen angebracht; auch kleine Wesen befinden sich darauf, die beobachten können. Nun führe unser Geist das Gerüst genau dem Eisenbahnzug nach, so daß also dieser von ihm aus gesehen ruhend, die ganze Erde aber als bewegt erscheint. In genau dem Augenblick, in dem das Eisenbahnunglück beginnt, stoppt unser Geist auch das Gerüst ab, so daß es in relativer Ruhe zum Eisenbahnzug bleibt. Die Gerüstwesen, die sich ausschließlich an ihre aufgetragenen Kilometerzahlen halten, bemerken nun natürlich eine mächtige Bewegung von Sonne, Mond und allen Sternen in der ursprünglichen Bewegungsrichtung des Gerüstes. Zwar bewegen sich diese regellos nach allen Richtungen; aber durch das Anhalten des Gerüstes ist natürlich die ihrer eignen Bewegung entgegengerichtete Komponente weggefallen.
Wie werden sie nun aber die Vorgänge im Zug deuten? Auf Trägheit werden sie sie nicht zurückführen können, denn er befand sich ja ihnen gegenüber dauernd in Ruhe! Sie werden also ein Gravitationsfeld annehmen, das die vorher bewegte Umgebung zur Ruhe brachte und im Zug alles durcheinander warf. Und worauf werden sie das Entstehen des Gravitationsfeldes zurückführen? Offenbar auf die von ihnen ja beobachtete starke Relativbewegung aller Himmelskörper gegen ihr System, die sie im Augenblicke des »Ruckes« des Systems wahrnehmen werden.
Wir besprechen nun einige Einwände, die man hiergegen machen kann. Zunächst könnte man sagen, daß diese plötzliche Einwirkung der doch sehr entfernten Himmelskörper ja eine zeitlose Fernwirkung darstelle, die doch eben von der neuen Theorie verpönt sei. Hierauf kann man nur mit dem Bedauern erwidern, daß wir unsern alten Äther nicht mehr besitzen. Hätten wir ihn noch, so könnten wir mit seiner Hilfe die Einsteinsche Auffassung leichter klarstellen. Wir könnten uns vorstellen, daß die entfernten Himmelskörper gewisse Spannungen im Äther zur Folge gehabt hätten, und daß diese Spannungen sich zwar nicht bei gleichförmiger, wohl aber bei ungleichförmiger Bewegung bemerkbar machen und somit das plötzliche Entstehen des Gravitationsfeldes veranlassen. Nun, wo wir den Äther nicht mehr zur Verfügung haben, müssen wir alles auf das »Feld« zurückführen, aber in der Sache wird nichts geändert. Neuerdings gebraucht übrigens Einstein, um für die wechselnde Eigenschaft des Feldes eine konkretere Bezeichnung zu haben, doch wieder den Ausdruck »Äther«, dem aber nach wie vor keinerlei stoffliche Eigenschaften zugesprochen werden dürfen. Freilich verhehlen manche sonst ganz gesinnungstüchtige Relativisten ihre Bedenken nicht, daß der eben erst aus der Physik »herausgeschmiss'ne Gast« nun schon wieder eingeführt werden soll. Der grausame Witz, daß man diese Sorte »Äther« eigentlich gerade so gut »avoir« nennen könne, stammt natürlich nicht von mir. – Wir können auch sagen, die ungleichförmige Bewegung unseres Lattensystems fand nicht nur statt gegen die jetzigen, sondern auch relativ zu den früheren Stellungen oder Bewegungen der Sterne. Wollen wir also unserm Zug dauernde Ruhe zuschreiben, wobei wir konsequenterweise eine ungleichförmige Bewegung der Sterne behaupten müssen, so können wir diese Bewegung als früher erfolgt annehmen, nämlich als zu der Zeit erfolgt, in der die Sterne dort standen, wo sie vom Zug aus während des Unglücks gesehen wurden. Und wenn sich nun die Wirkung auf den Eisenbahnzug scheinbar momentan geltend macht, so ist das demnach keine Verletzung des Prinzips der Nahewirkung, keine Behauptung zeitlos wirkender Fernkräfte.
Ferner könnte man sagen: Es ist doch höchst sonderbar, daß unser physikalischer Weltgeist ausgerechnet in dem Augenblick sein Gerüst anhielt, wo der Zug den Stein auf den Schienen fand. Darauf ist zu erwidern: Natürlich können wir uns die ungleichförmige Bewegung des Lattensystems auch in jedem andern Zeitpunkt erfolgt denken. Dann werden Zug, Schienen und Landschaft dem entstehenden Gravitationsfeld völlig ungehindert nachgeben, der Eisenbahnzug, indem er sofort zu fallen anfängt, Schienen und Landschaft, indem sie ihre nunmehr ja nach »oben« gerichtete Bewegung verlangsamen. Relativ bleibt also alles ungeändert, und physikalisch geschieht einfach gar nichts. Diese Überlegung zeigt, daß es auch vom Standpunkt der allgemeinen Relativitätstheorie nicht etwa der Ruck des Lattensystems war, der den Zug verunglücken ließ, sondern nur der Stein auf den Schienen, der ihn am »Fallen« hinderte. Und was das unmotivierte Zusammentreffen zwischen dem Stein auf den Schienen und dem Ruck des Systems anlangt, so kommt hier die Willkürlichkeit unserer ursprünglichen Annahme zum Ausdruck. Es ist eben, auf deutsch gesagt, ziemlich verrückt, anzunehmen, daß der verunglückte Eisenbahnzug dauernd in Ruhe geblieben sei; das Beispiel stammt ja auch von einem Gegner der Relativitätstheorie, der ihr damit einen Knüppel zwischen die Beine werfen wollte. Es würde gewiß keinen Ruhmestitel unserer Lehre ausmachen, wenn sie die Verifizierung einer solchen, fast absurd zu nennenden Voraussetzung sozusagen aus dem Ärmel schütteln könnte. In der Willkür, die sie bei der Durcharbeitung zu Hilfe nehmen muß, zeigt auch sie eben die völlige Unnatur des eingenommenen Standpunktes.
Schließlich kann man Anstoß nehmen an den plötzlich entstehenden Gravitationsfeldern. Dies ist nun freilich der Kernpunkt der ganzen Theorie: die Behauptung, daß stark bewegte, wenn auch noch so ferne Massen durch ihre Relativbewegung eine weit stärkere Gravitationswirkung auszuüben vermögen, als es die bisherige Newtonsche Auffassung zuläßt. Auch unser Abschnitt über die Zentrifugalkräfte auf der Erde führte schließlich auf diesen entscheidenden Punkt. Für die Trägheit, nämlich für die auf der Erde wirkenden Zentrifugalkräfte, haben die Sterne insofern ganz sicher Bedeutung, als wir ja bloß an ihnen die ganze Rotationsbewegung der Erde feststellen können. Bei der sonstigen völligen Äquivalenz von Trägheit und Schwere erscheint es also nur konsequent, ihnen auch Schwerewirkungen zuzuschreiben.
Ein Einwand gegen unsere Darstellung ist natürlich möglich: Man kann sagen, die angenommenen Gerüstwesen werden beim plötzlichen Anhalten des Gerüstes auch ihrerseits den Ruck verspüren, hinpurzeln und sich somit auch über das gleiche Schicksal des Eisenbahnzugs weder wundern, noch Gravitationsfelder und dergleichen zur Begründung heranziehen.
Wer so spricht, steht eben auf dem Standpunkt einer Raumwirkung an sich, einer absoluten Raumauffassung. Und dieser ist natürlich zuzubilligen, daß sie in sich ebenso logisch und widerspruchsfrei ist wie die relativistische. Mit den Mitteln der Logik und auch der verschärften Logik, der mathematischen Analyse, kann zwischen beiden Anschauungen nicht entschieden werden. Nicht die Logik, sondern eine Art Instinkt, eine Intuition war es, die Einstein und schon lange vor ihm Mach der relativistischen den Vorzug geben ließen. Auf die Dauer freilich wird es nun mit Instinkt und Intuition nicht getan sein: die Tatsachen müssen entscheiden, und zu ihrer kurzen Würdigung wollen wir uns nun wenden.
Wenn sich auch unsere Schrift, schon um dem Leser die neuen Gedankengänge nahezubringen, auf den Boden der Relativitätstheorie stellen mußte, so würde es sich doch nicht rechtfertigen lassen, sie nun als eine endgültig durch Beobachtungen bewiesene Tatsache zu behandeln. Es wäre ja dann auch unverständlich, daß einzelne hochangesehene Gelehrte, wie z. B. der Münchener Astronom v. Seeliger, der Heidelberger Physiker Lenard u. a., unsere Theorie entschieden ablehnen. Die Haltung der Mehrzahl der Physiker und auch Mathematiker ist allerdings wesentlich freundlicher. Wir wollen möglichst objektiv zusammenstellen, was an Tatsachen etwa für oder gegen die Relativität geltend gemacht werden kann.
Die Abweichung in der Periheldrehung des Merkur war oben schon besprochen. So klein sie ist, gilt sie doch als ganz zuverlässig erwiesen, und kein Geringerer als Leverrier, der Entdecker des Neptun, hatte ihren Betrag bereits errechnet. Lehnt man die Einsteinsche Erklärung ab, so gerät man in eine schwierige Lage. Es ist nicht abzusehen, wie sie mit dem Newtonschen Gesetz anders in Einklang gebracht werden könnte als durch Auffindung des intramerkuriellen Planeten. Der ist nun trotz aller Mühe nie gesehen worden. Es bliebe noch die Möglichkeit, daß dieser Planet aus einer Masse ganz fein verteilten Staubs bestünde, und man hat geglaubt, auf diese Weise vielleicht auch noch eine andere rätselhafte Erscheinung aufklären zu können, nämlich das Zodiakallicht. Doch ist eine bestimmte Theorie, die natürlich über Masse, Ausdehnung, Lage usw. dieser hypothetischen Staubwolke bestimmte Annahmen machen und sie an Hand der Beobachtungen, insbesondere der Zodiakallichterscheinung, prüfen müßte, bisher nicht aufgestellt. Aber die allgemeine Möglichkeit, daß ein bisher noch nicht beachteter Umstand vielleicht doch noch eine Übereinstimmung mit dem Newtonschen Gesetz ermöglicht, kann natürlich nicht ohne weiteres von der Hand gewiesen werden.
Die Ablenkung der Lichtstrahlen durch die Sonne kann nun ganz unbedingt ein sehr starkes psychologisches Moment für sich beanspruchen: die Theorie ist hier der Beobachtung vorausgeeilt. Wollte man etwa den Verdacht äußern, daß Einstein seine Formeln eben im Hinblick auf die Perihelbewegung des Merkur »zurechtgemacht« habe, so ist ein ebensolcher Verdacht völlig unmöglich gegenüber der Ablenkung der Lichtstrahlen. Denn von ihr war vor Einstein absolut nichts bekannt. Es ist merkwürdig, aber doch Tatsache: So viele, auch von kundigen Astronomen hergestellte photographischen Aufnahmen totaler Sonnenfinsternisse bei dem großen Wert, der von jeher auf die Beobachtung dieses seltenen Phänomens gelegt worden war, auch existierten, es fand sich unter ihnen nicht eine einzige, bei der eine Prüfung der behaupteten Wirkung möglich gewesen wäre. So mußte eben eine neue Finsternis abgewartet werden, die dann Mai 1919 eintrat.
Die nun vorgenommenen Aufnahmen und mikroskopischen Messungen auf der Platte bestätigten im großen und ganzen Einsteins Vorausberechnungen, zeigten jedoch auch nicht ganz unerhebliche Abweichungen.
Wir lassen hier die Zahlen nach einer Mitteilung v. Laues in den »Naturwissenschaften« 1920 S. 391 folgen (vgl. dazu auch die ausführliche Veröffentlichung von E. Freundlich a. a. O. S. 667):
| Stern Nr. *) | Verrückung in Bogensekunden in der Richtung | |||
| von S. nach N. | von O. nach W. | |||
| beobachtet | berechnet | beobachtet | berechnet | |
| 11 | +0,16 | +0,02 | -0,19 | -0,22 |
| 5 | -0,46 | -0,43 | -0,29 | -0,31 |
| 4 | +0,83 | +0,74 | -0,11 | -0,10 |
| 3 | +1,00 | +0,87 | -0,20 | -0,12 |
| 6 | +0,57 | +0,40 | -0,10 | +0,04 |
| 10 | +0,35 | +0,32 | -0,08 | +0,09 |
| 2 | -0,27 | -0,09 | +0,95 | +0,85 |
*) Stern Nr. 1 fehlt, weil er infolge der Sonnenkorona nicht genügend deutlich wurde, 7, 8, 9 aus anderen Gründen. Die Sterne sind nach ihrer Sonnennähe geordnet.
Zur Bewertung wolle man sich immer wieder vorstellen, daß eine Sekunde dem Winkel entspricht, unter dem 1 mm aus einer Entfernung von 200 m erscheint! – An dem Bestehen der Ablenkung ist natürlich nicht zu zweifeln. Aber es wurde nun der Einwand erhoben, daß sie von der Strahlenbrechung in der Sonnenatmosphäre herrühre. Eine solche besteht allerdings sicher, so weit die Sonnenatmosphäre reicht. Ihre Größe würde abhängen von der Beschaffenheit, der Dichtigkeit, der Temperatur usw. des Gases.
Über alle diese Größen auch nur einigermaßen sichere, von der gegenwärtigen Beobachtung unabhängige Daten zu erhalten und mit ihrer Hilfe eine Theorie aufzustellen, die dann durch obige Zahlen als richtig zu bestätigen wäre, ist wohl ganz ausgeschlossen. Wohl aber könnte man aus den Beobachtungszahlen die notwendigen Annahmen über jene Daten der Sonnenatmosphäre herleiten. Aber auch dann würden Theorie und Praxis kaum besser übereinstimmen als in der Einsteinschen, doch vor der Beobachtung aufgestellten Theorie. Auch macht E. Freundlich wohl mit Recht darauf aufmerksam, daß bei Annahme einer so ausgedehnten Sonnenatmosphäre mindestens nach unsern irdischen Erfahrungen zu urteilen das Sternenlicht sehr viel stärker absorbiert werden würde, als es die Beobachtung zeigte. Ja, nach seiner Behauptung würden dann die meisten der abgelenkten Sterne überhaupt nicht mehr auf der photographischen Platte erschienen sein.
Noch andere Erklärungsversuche für die Ablenkung sind gemacht worden, auch die Zurückführung auf Erscheinungen, die wie die von Courvoisier angenommene sogenannte »jährliche Refraktion« zwar selbst noch höchst unsicher und umstritten sind, auch selbst im günstigsten Fall die Ablenkung nur zum Teil zu erklären vermöchten.
Wie die Dinge liegen, ist es wohl natürlicher, den Einstein-Effekt als reell anzusprechen und eher die Abweichung, die die Beobachtung zeigte, auf den Einfluß einer noch unbekannten Strahlenbrechung oder anderweitige Nebenumstände zurückzuführen.
Eine besonders große Rolle spielt in der letzten Zeit in der öffentlichen Erörterung eine dritte Möglichkeit, die Relativitätstheorie durch Beobachtungen zu bestätigen: die Frage der sogenannten »Rotverschiebung der Spektrallinien«. Es hat damit folgende Bewandtnis: Bekanntlich folgen die Wellen einfarbigen Lichtes aufeinander in ganz regelmäßigen, ganz außerordentlich kurzen Zeitabständen. Eben wegen ihrer Regelmäßigkeit wären sie nun durchaus geeignet, als Zeitmesser, kurz gesagt, als Uhren zu dienen. Nun ist, wie wir wissen, auch der Gang der Uhren von ihrem Bewegungszustand abhängig; beschleunigte Bewegungen können aber, wie wir gesehen haben, durch Gravitationsfelder ersetzt werden; auch diese müssen also einen Einfluß auf den Uhrengang haben, und es wäre nicht schwer, zu zeigen, was uns hier freilich zu weit führen würde, daß alle Gravitationsfelder verzögernd auf den Uhrengang einwirken. Was nun die Lichtschwingungen anlangt, so sind hier die roten die langsamsten des Spektrums. Eine Verschiebung des Spektrums nach dem roten Ende hin entspricht also einer Verzögerung des Uhrengangs. Gemessen werden kann diese Verschiebung nur an den in ihm auftretenden Linien, den sogenannten Fraunhoferschen Linien. Die Relativitätstheorie verlangt also zu ihrer Bestätigung den Nachweis, daß die Fraunhoferschen Spektrallinien, falls sie von Sternen mit starkem Gravitationsfeld herrühren, sich nach dem roten Ende hin verschieben.
Die große Schwierigkeit eines solchen Nachweises beruht nun darin, daß auch durch Bewegung im Sinne sich vergrößernder Entfernung eine solche Rotverschiebung eintritt. Denn in diesem Falle wird das Auge in der gleichen Zeit von weniger Schwingungen getroffen, als wenn die Lichtquelle ruhte; auch dann scheinen die Schwingungen langsamer zu werden, eine Rotverschiebung der Spektrallinien tritt ein. Die Trennung dieser von der Relativitätstheorie unabhängigen Erscheinung, »dem Dopplereffekt«, von dem erwarteten Einsteineffekt macht nun große praktische Schwierigkeiten. Ihre Lösung wäre am ersten beim Sonnenspektrum zu erwarten, weil die Bewegung der Sonne gegen die Erde genau bekannt ist, also berücksichtigt werden kann. Trotzdem ist die Erscheinung noch nicht unzweifelhaft sicher nachgewiesen; die verschiedenen Beobachtungen stimmen noch nicht recht miteinander überein; eine endgültige Lösung dieser Frage ist wohl in den nächsten Jahren zu erwarten.
Allzu groß ist also der Tatsachenkreis, der eine unmittelbare Nachprüfung durch das Experiment gestattet, zweifellos nicht. Überblickt man ihn, so kann man sagen, daß jedenfalls keine einzige Tatsache bekannt ist, die der Relativitätstheorie widerspräche, dagegen mehrere, die der alten Auffassung mindestens Schwierigkeiten machen. Andrerseits muß man aber wohl zugeben: Angenommen, es wären Tatsachen von nicht größerem Umfang und in nicht größerer Zahl als die besprochenen gegen ein anerkanntes Naturgesetz, sagen wir etwa das Energieprinzip, bekannt geworden, so würden wir uns ganz zweifellos nicht veranlaßt sehen, ein sonst so glänzend bewährtes Gesetz deswegen aufzugeben; es würde mit allen Kräften an der Aufhellung des Widerspruchs gearbeitet, schlimmstenfalls aber seine Beseitigung der Zukunft überlassen werden.
Ähnlich steht die Sache in unserm Fall. Wer die alte, absolute Raum- und Zeitauffassung für so bewährt hält, daß er sich um einiger in dem unendlichen Tatsachenbereich der Wissenschaft fast verschwindender Einzelheiten willen von ihr nicht zu trennen vermag, dem ist es nicht zu verübeln, daß er eine vielleicht lange Jahrzehnte hindurch gehegte Überzeugung nicht sofort preisgeben will. Nicht wenige philosophisch gerichtete Physiker aber, wie vor allem die Anhänger des 1915 verstorbenen Ernst Mach, als deren Wortführer wir wohl Petzoldt ansprechen dürfen, halten von vornherein die relativistische Auffassung für die unvergleichlich vollkommenere.
Ähnlich steht es auch mit der mathematischen Seite der Theorie. Schon lange vor Einstein war von Mathematikern, insbesondere von Riemann, eine Raumauffassung vertreten worden, die mit den Anforderungen der Einsteinschen Physik durchaus übereinstimmt. Als im zweiten Jahrhundert v. Chr. der glänzende griechische Geometer Apollonius sein Buch über Kegelschnitte schrieb, konnten platt aufs Nützliche gerichtete Geister wohl fragen, was die Untersuchung solcher in der Natur nicht vorkommenden Kurven denn für einen »Zweck« habe. Der »Zweck« fand sich, als Kepler 18 Jahrhunderte später seine Gesetze aufstellte. Ganz ähnlich steht es, einmal die Richtigkeit der Relativitätstheorie vorausgesetzt, mit dem Verhältnis der Einsteinschen Physik zu den Riemannschen mathematischen Spekulationen. (Vgl. über diese sehr interessanten Dinge auch das Literaturverzeichnis.) Damit erledigt sich auch der Vorwurf des Plagiates, der Einstein gegenüber Mach, Riemann u. a. gemacht wurde. Es ist ungefähr so sinnvoll, als wenn man Kepler vorwerfen wollte, er habe von Apollonius, oder Richard Wagner, er habe von Schopenhauer »abgeschrieben«, deswegen, weil in der Tat der Geist Wagnerscher Musik und der Schopenhauerscher Philosophie durchaus übereinstimmen.
Wertvolle Anregung zu diesem Kapitel gaben mir wiederholte Unterhaltungen mit Herrn Prof. Dr. Böhmer (Dresden).
Von den Schlüssen, die Einstein aus seiner veränderten Raum- und Zeitauffassung zog, hat keiner solches Aufsehen erregt wie der, der die Unendlichkeit der Welt bestreitet und statt ihrer ein zwar grenzenloses, aber in sich geschlossenes, endliches Universum behauptet. Wollen wir in diese Fragen eindringen, so ist es wohl am besten, an ein Bild anzuknüpfen, das Helmholtz in seiner berühmten Abhandlung: »Über die geometrischen Axiome« gebraucht hat. Er spricht dort von gedachten »Flächenwesen«, die nur in zwei Dimensionen, also beispielsweise in einer Ebene leben, alle Sinneseindrücke nur aufnehmen können, sofern sie aus dieser Ebene stammen, allen aus der dritten Dimension herrührenden Vorgängen hingegen völlig gefühllos gegenüberständen. Sie würden es beispielsweise nicht merken, wenn man sie von oben mit einem Stein bewirft! Freunden solcher Spekulationen möchte ich übrigens den satirischen Aufsatz Fechners: »Der Schatten ist lebendig« (siehe S. 52 Fußnote) empfehlen.
Wir wollen noch die Zusatzhypothese machen, daß diesen Wesen nur ein kleines Gebiet, sagen wir ein Garten, zur Verfügung steht. Im Verhältnis zur Erde ist das immer noch viel mehr, als der uns Menschen im Vergleich zur Sternenwelt erreichbare Raum. Nun sei unter diesen Wesen ein Streit darüber ausgebrochen, ob sie eigentlich auf einer Ebene oder auf einer Kugeloberfläche wohnen; die Mehrheit entscheide sich für eine Ebene, die Minderheit, unter ihnen aber gerade die schlaueren Köpfe, für eine Kugeloberfläche. Die Entscheidung wird sehr schwer sein, aus folgenden Gründen: Wir als dreidimensionale Wesen erkennen sofort den Unterschied zwischen Ebene und Kugeloberfläche in der Anschauung. Aber dazu ist eben die dritte Dimension durchaus notwendig! Stellen wir uns ein eindimensionales Wesen vor, das sich etwa durch Streckung und Zusammenziehung, ungefähr wie ein Regenwurm, nur ganz streng linienförmig gedacht, vorwärtsschiebt. Der Unterschied zwischen einer geraden und einer krummen Linie wird einem solchen Wesen offenbar nie anschaulich werden können. Denn alle Definitionen oder Operationen, die eine gerade Linie als solche auszeichnen – kürzeste Verbindung zwischen zwei Punkten; Linie, die beim Umklappen mit sich selbst in Deckung bleibt –, setzen mindestens eine Fläche voraus. Ebenso kann auch der Unterschied zwischen einer Ebene und einer krummen Fläche nicht im zweidimensionalen Gebiet veranschaulicht werden. Hierzu wäre es durchaus nötig, sie in den dreidimensionalen Raum sozusagen einzubetten. Auch mit den Mitteln mathematischer Deduktion ist die Frage, ob Ebene oder Kugeloberfläche, nicht zu lösen. In sich widerspruchslose Gebilde sind beide, beide existieren demnach in mathematischem Sinn. Bei unserer Voraussetzung einer nur beschränkten Bewegungsfreiheit unserer zweidimensionalen Wesen auf der Kugeloberfläche ist eine Entscheidung überhaupt nicht zu treffen.
Nun wollen wir sogar noch diese Beschränkung fallen lassen und unseren zweidimensionalen Freunden eine erhebliche Reisefreiheit einräumen. Nur Erdumseglung allerdings sei ihnen noch nicht gestattet. Nun, wird man denken, kann ihnen eine Entscheidung über die mathematische Natur ihrer Heimat nicht schwer fallen; zwar eine anschauliche Darlegung des Unterschieds der beiden möglichen Auffassungen ist auch jetzt noch, wie wir wissen, ausgeschlossen. Aber trotzdem, sollte man denken, ist die Erledigung der Frage nicht schwer. Eine Krümmung der Erdoberfläche läßt sich ja sehr leicht feststellen, auch wenn wir die bekannten, oft gehörten Gründe, daß bei Schiffen die Mastspitzen zuerst sichtbar werden, daß der Horizont sich auf Bergen erweitert usw., nicht gelten lassen, weil sie ja dreidimensionale Anschauung voraussetzen. Aber man braucht ja nur die Winkel eines beliebigen Dreiecks nachzumessen; in der Ebene ist ihre Summe bekanntlich stets gleich zwei Rechten. Auf der Kugeloberfläche aber können die Linien keine Geraden im gewöhnlichen Sinne sein; nehmen wir an, sie würden durch Spannung von Fäden erhalten, so würde sich nun die Winkelsumme stets größer als zwei Rechte herausstellen. Bei der Ausmessung der Winkel aber werden keinerlei dreidimensionale Vorstellungen zu Hilfe genommen, sie ist jenen Wesen also durchaus möglich.
Aber nun kommt der Hauptpunkt. Der Fundamentalsatz, daß die Winkel im Dreieck zwei Rechte betragen, gilt nur in der euklidischen Geometrie. In einer nichteuklidischen, die in sich gleichfalls durchaus logisch ist, kann die Summe größer sein. Sollten also jene Wesen beim Ausmessen der Winkel eines Dreiecks mehr als zwei Rechte feststellen, so hätten sie immer noch völlige Freiheit, zu entscheiden: Aha! Endlich ist bewiesen, daß der alte Herr Euklid doch unrecht hatte. Wir sehen's ja, daß die Dreieckswinkel nicht zwei Rechte ausmachen, wie er es uns hat glauben machen wollen, sondern mehr. Oder auch: Euklid hat selbstverständlich recht, und wir wissen nun endlich, daß wir auf einer Kugeloberfläche wohnen. Es ist kaum nötig, hinzuzufügen, daß bei Annahme einer Ebene eine unendlich große Welt, im Fall einer Kugeloberfläche eine zwar grenzenlose, in sich geschlossene, aber doch endliche Welt angenommen wird.
Wir sehen also: Die Geometrie ist sozusagen der Maßstab, mit dem gemessen wird, und je nach seiner Wahl ist eine endliche oder eine unendliche Welt das Ergebnis. Folgende Überlegung macht dies vielleicht noch etwas deutlicher: Wir sind gewohnt, daß Maßstäbe absolut unveränderlich, wie man sagt »starr« bleiben. Nichtsdestoweniger ist diese Annahme vom Standpunkte der Relativitätstheorie aus durchaus willkürlich. Von uns aus gesehen sind in obenstehender Figur die Strecken PA, AB, BC und auch PD, DE, EF, FG alle gleich groß, während die entsprechenden Strecken PA', A'B', BC' und PD', D'E', E'F', F'G' von P aus nach beiden Seiten größer werden. Nehmen wir nun an, es gehe ein Mann auf der geraden Linie und messe mit einem Maßstab, der immer wachse, je weiter er sich von P entfernt. Ihm werden dann die Strecken PA', A'B', B'C' usw. alle gleich groß erscheinen. Seine Maßresultate sind also dieselben wie die unseren auf dem Kreis; findet er dieses Ergebnis, das unsere Figur nur in einer Richtung andeutet, in allen Richtungen, so wird er die gerade Linie für gebogen und die Ebene für eine Kugeloberfläche halten. Nehmen wir umgekehrt einen Beobachter an, der auf dem Kreis von P aus mit einem sich ständig verkürzenden Maßstab mißt; die gleichen Strecken PA, AB, BC usw. scheinen sich ihm dann ebenso zu dehnen, wie uns PA', A'B', BC', er wird also wähnen, von P aus auf einer geraden Linie zu wandern und dementsprechend die endliche Kugeloberfläche als eine unendliche Ebene erklären.
Wir sehen also: Es ist eine Frage der gewählten Geometrie und der damit zusammenhängenden Prinzipien der Messung, ob ich dieselbe Fläche als unendliche Ebene oder als endliche Kugeloberfläche deuten will.
Nun erst kehren wir von den Helmholtzschen Flächenwesen zu unserem dreidimensionalen Problem zurück. Hier versagt natürlich die Anschauung vollkommen. Denn wollten wir den Unterschied von dem unendlichen euklidischen Raum und einem endlichen geschlossenen Raum, der im dreidimensionalen Gebiet der zweidimensionalen Kugeloberfläche entsprechen würde, anschaulich vorführen, so wäre die Einbettung in den vierdimensionalen Raum ebenso erforderlich, wie bei jener Vorfrage in den dreidimensionalen. Unserer Anschauung steht aber der vierdimensionale Raum in keiner Richtung zur Verfügung, auch nicht als Hilfsvorstellung.
Es ist für den Mathematiker eine längst bekannte Tatsache, daß es verschiedene Geometrieen gibt, je nach den Axiomen, die zugrunde gelegt werden, und die ja, mathematisch betrachtet, willkürlich sind. Die Wahl der Geometrie entscheidet aber, wie das Vorangegangene zeigte, über die Auffassung unseres Raumes. Unter der Voraussetzung einer einigermaßen gleichmäßigen Erfüllung des Raumes durch Materie erfordert die Allgemeine Relativitätstheorie eine Riemannsche und nicht eine Euklidische Geometrie. Sie verlangt ferner einen endlichen, in sich geschlossenen Raum. Es würde uns indessen zu weit führen, auseinanderzusetzen, warum trotz der engen Verbindung zwischen Raum und Zeit hieraus keineswegs die Endlichkeit der Zeit folgt, wie dies mitunter irrtümlich behauptet wird.
Nun liegt freilich ein Einwand nahe. Man könnte sagen: Ich postuliere eben eine euklidische Welt, denke in ihrer Mitte ein großes rechtwinkliges Achsenkreuz und setze meinen Kilometermaßstab einmal über das andere Mal an; was kann dabei Schlimmes passieren? Ich kann doch auch nicht auf Bretter stoßen, mit denen die Welt vernagelt ist, das Messen geht immer weiter, und somit ist eben die Welt unendlich. Hierauf ist zu erwidern: Der Standpunkt ist rein mathematisch absolut unwiderleglich; die geometrische Widerspruchslosigkeit des euklidischen Raumes kann niemand bezweifeln; es fragt sich nur, ob er physikalisch zweckmäßig ist. Wenn z. B. die Linien, längs denen wir unseren Maßstab anlegen, nicht die sind, auf denen sich das Licht bewegt, auch nicht die, auf denen ein sich selbst überlassener Körper weiterfliegt, so werden wir stutzig werden und uns fragen, mit welchem Recht wir sie dann noch als »Gerade« bezeichnen, und ob es nicht geratener ist, die Geometrie zu wechseln, statt die ganze Physik auf den Kopf zu stellen. Hierzu kommt noch folgendes:
Die Welt ist nicht stetig! Sie weist vielmehr im großen Weltkörper auf und im kleinen Atome. Nehmen wir nun an, unser euklidischer Beobachter sei mit seinem Kilometermaßstab in die Welt geschickt worden, um sie auszumessen. Er durchwandert zunächst die nähere Umgebung des Sonnensystems, sagen wir einige hundert Lichtjahre. Er stellt bei dieser Gelegenheit eine gewisse Durchschnittsgröße der Sterne fest. Nun erst wandert er frei ins Universum hinaus. Wenn nun beim Weiterschreiten durchschnittlich, von individuellen Verschiedenheiten abgesehen, die Sterne immer größer und größer werden, so wird der Mann sich sagen: Hier stimmt was nicht! Warum soll denn in der ganzen großen Welt gerade mein Ausgangspunkt die Eigentümlichkeit haben, daß von ihm aus betrachtet die Weltkörper immer wachsen und wachsen, je weiter ich komme. Es wird wohl am Maßstab liegen! Der wird offenbar immer kleiner und kleiner und spiegelt mir so das Größerwerden der Sterne und die Unendlichkeit der Welt bloß vor. Nehme ich, wie in obiger Figur, an, ich befinde mich auf der gebogenen und in sich geschlossenen, statt der geraden, ins Unendliche verlaufenden Linie, so hören die offenbar unnatürlichen Zerrungen sofort auf. Und wie mit den Himmelskörpern im großen, so steht es mit den Atomen im kleinen. Denn daß alle Himmelskörper Atome aufweisen, die mit den unseren identisch sind, kann nach den Ergebnissen der Spektroskopie als bewiesen gelten. So kann also nur die physikalische, niemals die rein mathematische Betrachtung die Frage nach der zu wählenden Geometrie und die damit zusammenhängende nach der Endlichkeit oder Unendlichkeit der Welt entscheiden. Wir haben sogar noch ein einfacheres Kriterium, als das oben angegebene: In einer endlichen Welt hat nur eine endliche Zahl von Himmelskörpern und demnach auch von Atomen Platz. Die Zahl der Himmelskörper im großen und der Atome im kleinen ist es also, die letzten Endes die Frage nach der Endlichkeit oder Unendlichkeit der Welt entscheiden muß. Diese Zahlen also muß die Allgemeine Relativitätstheorie, und das ist in der Tat ihre merkwürdigste Folgerung, als endlich annehmen.
Einstein hat sogar eine Formel für die Größe seines Weltraums angegeben; sie setzt aber die Kenntnis der durchschnittlichen Massenverteilung in der Welt voraus, über welche Größe doch nur recht unsichere Annahmen gemacht werden können.
Es scheint, als ob die Einsteinsche Auffassung die Astronomie aus einer sonst peinlichen Verlegenheit befreien könnte. Nimmt man nämlich an, daß der Raum unendlich groß ist, und daß die Sterne in ihm durchschnittlich gleichmäßig verteilt seien – lokale Unregelmäßigkeiten können wir sogar noch zulassen –, so gerät man in eine eigentümliche Schwierigkeit. Wir denken uns um uns als Mittelpunkt eine Kugel von so großem Radius beschrieben, daß kleinere Ungleichheiten ausgeglichen sind. Die in ihm vorhandenen Sterne senden uns eine gewisse Menge Licht. Nun nehmen wir den Kugelradius doppelt so groß. Jetzt wird jeder Stern durchschnittlich die doppelte Entfernung aufweisen, sein Licht also nur im vierten Teil seiner vorigen Stärke wahrgenommen werden. Aber dafür hat sich der Rauminhalt der Kugel und mit ihm, wenn wir von der Voraussetzung gleichmäßiger Verteilung ausgehen, die Anzahl der Sterne verachtfacht; das uns gelieferte Licht wird sich also immerhin verdoppelt haben. Und da wir natürlich in dieser Weise fortfahren können, den Radius der Kugel, wie groß er auch immer gewesen sein mag, wiederum verdoppeln, verdreifachen, vervierfachen können, so müßte schließlich jede Stelle des ganzen Himmels durchschnittlich in Sonnenhelligkeit erstrahlen. Um dieser natürlich unmöglichen Folgerung zu entgehen, müßte man seine Zuflucht zu dunkeln Massen oder einer Lichtabsorption des Raumes, jedenfalls zu einer ad hoc erfundenen Hypothese nehmen. Auch dann würde die entsprechende Schwierigkeit bezüglich der Gravitationswirkung der Sterne bestehen bleiben. Danach muß also die Astronomie ohnehin von der Annahme einer gleichmäßigen Verteilung aller Sterne bis in alle Unendlichkeit absehen.
Freilich können alle diese Spekulationen nur mit einem Fragezeichen geschlossen werden, das schon aus allgemeinen erkenntnistheoretischen Gründen offen bleiben muß. Sie gelten ja auch nur unter der Voraussetzung einer gleichmäßigen Erfüllung des Raumes durch Materie, einer Annahme, die weder astronomisch nachprüfbar, noch auch mit den Grundlagen der Allgemeinen Relativitätstheorie in einem notwendigen Zusammenhang steht. Wenn ich trotz erheblicher Bedenken das vorstehende Kapitel aufgenommen habe, so geschah dies nicht nur, weil sein Fehlen in den früheren Auflagen von sehr hochgeschätzter Seite als Mangel empfunden wurde, sondern auch, weil diese Fragen tatsächlich das allgemeine Interesse in ungewöhnlich starkem Maße erregt haben, der Leser eine Stellungnahme zu ihnen also erwarten darf. Auch scheinen sie mir in andern populären Schriften über unser Thema nicht durchweg mit der gerade hier notwendigen Vorsicht behandelt zu sein.
In der Bewunderung des Scharfsinns und noch mehr der fabelhaften geistigen Selbständigkeit eines Lorentz, Minkowski und vor allem Einstein ist sich wohl alle Welt einig. Aber mehr als an solchen Werturteilen wird dem Leser an einer sachlichen Charakterisierung der Leistung dieser Forscher liegen, die am besten durch einen Vergleich gegeben wird. Er ist denn auch schon längst gefunden. Von allen Großtaten im Gebiet der Naturwissenschaft hat keine mit der Einsteins so viel Ähnlichkeit wie die des Kopernikus, wobei es uns auch wieder mehr auf Hervorhebung sachlicher Gesichtspunkte als auf Werturteile ankommt. Wie mir scheint, geht der Vergleich sehr viel weiter, als gemeinhin angenommen wird, und das liegt an einer meist unrichtigen Beurteilung, nun aber nicht etwa der Relativitätstheorie, sondern des Kopernikus. Der Nichtastronom denkt vielfach, daß es die einzige oder doch wenigstens die Hauptaufgabe der Astronomie sei, festzustellen, ob sich die Erde bewege, und da Kopernikus diese Aufgabe endgültig gelöst habe, so sei er eben »der« Astronom für alle Zeiten. Aber von dieser Auffassung kann natürlich gar keine Rede sein. Die Astronomie hat wie jede andere Naturwissenschaft die Aufgabe, zu beobachten und die Beobachtungen, grundsätzlich gesammelt und geordnet, in einer Theorie wiederzugeben. Die zweite Aufgabe leistete die Astronomie jener Zeit in einer für heutige Begriffe nur sehr mangelhaften Weise, und es liegt an dem kinematischen Relativitätsprinzip, daß die Kopernikanische Auffassung ihr dabei kaum helfen konnte. Was diese für sich geltend machen konnte, war natürlich auch nicht eine bessere Einordnung der Tatsachen in die Theorie, sondern nur eine außerordentliche Vereinheitlichung der gesamten Theorie durch prinzipielle Hervorkehrung eines völlig neuen Gesichtspunktes. Dabei hätten große Teile nicht etwa nur der praktischen, sondern auch der theoretischen Astronomie durch den neuen Gesichtspunkt ganz unverändert bleiben und vollständig in die neue, Kopernikanische Theorie mitübernommen werden können. Ganz ebenso wird es sehr großen Teilen der Physik und fast der gesamten Astronomie gegenüber der Relativitätstheorie gehen. Was beide Anschauungen zunächst für sich geltend machen konnten, waren nicht etwa in erster Linie Tatsachen, sondern das große innere Gewicht, das die Vereinheitlichung und Vereinfachung der ganzen Theorie für sich geltend machen konnte. Wurden nun aber endlich wirklich schlüssige Beweise verlangt, so ist es für beide Theorien, die doch so fundamental umstürzend wirkten, überaus bezeichnend, daß die Beweise nur in der Beobachtung ganz winziger, nur eben noch wahrnehmbarer Größen gefunden werden konnten. Der erste wirkliche »Beweis« für die Kopernikanische Theorie lag in der Feststellung der jährlichen Periode der Aberration, die wir S. 40 besprachen und die erst einem geübten Beobachter mit einem leistungsfähigen Fernrohr gelingen konnte. Solch winzige Größen können schließlich Bedeutung gewinnen, selbst in den großen Fragen der Weltanschauung.
Wenn nun häufig eingewandt wird, daß die Frage der Relativitätstheorie nie so einschneidend werden könne für die Fragen der Weltanschauung wie die des heliozentrischen oder geozentrischen Systems, und daß sie ferner für das große Publikum auch schon deswegen keine allzu große Bedeutung gewinnen könne, weil sie dafür viel zu schwerverständlich sei, so muß erwidert werden, daß es ebenso schwer ist, sich vorzustellen, was im Reformationszeitalter ein Durchschnittskopf von Kopernikus verstanden haben mag, als vorauszusagen, wie weitgehend in einigen Jahrhunderten die Relativitätstheorie die Gemüter beeinflußt haben wird. Was einschneidender ist, die allerdings außerordentlich eindrucksvolle, sozusagen »extensive« Umstellung des Sonnensystems, oder die vielleicht weniger großartige, aber doch sehr tief eindringende »intensive« Umdeutung unserer Raum- und Zeitvorstellung, können wir dahingestellt sein lassen. Worauf es in erster Linie ankommt, ist das, daß beide Lehren den Mut fanden, um einer Vereinfachung und Vereinheitlichung der Theorie willen einen als absolut überkommenen Begriff zu relativieren. Denn auch in des Kopernikus Leistung ist das Große die Relativierung des Begriffs der Ruhe, der früher in der ruhenden Erde als schlechthin absolut erschien.
Auch die Widerstände, die sich gegen beide Fortschritte geltend machen, sind ganz ähnlicher Art. Gerade die Relativierung des früher absolut Gesetzten empfindet das öffentliche Bewußtsein als eine Vernichtung psychologischer Werte und setzt sich zur Wehr. Alltägliche Erfahrungen, dort die der Ruhe der Erde, hier die der Starrheit der Raum- und Zeitmaßstäbe, machen sich mit immer erneuter Wucht geltend und beanspruchen unbedingte Gültigkeit weit über das Gebiet ihrer ursprünglichen Erfahrung hinaus. Und hiergegen führt die von der Theorie unterstützte Kritik ihren zähen Kampf. Ob dieser auch bei der Relativitätstheorie mit einem endgültigen und vollen Sieg der neuen Ideen enden wird, muß die Zukunft lehren. In einem Punkte freilich wird ihr wohl ein leichterer Kampf beschieden sein als seinerzeit der Kopernikanischen Lehre: Nicht das wurde Kopernikus in erster Linie verübelt, daß er die Erde sich bewegen ließ, insofern diese ein physikalisches System darstellte; vielmehr wurde die Erde auch als religiöser Begriff betrachtet. Daß der Schemel der Füße Gottes, der Schauplatz der Taten des Welterlösers, nicht mehr sein sollte als Venus oder Mars, das verletzte die Zeitgenossen Luthers in ihren tiefsten Tiefen. Gegen wirkliche oder vermeintliche Werte dieser Art braucht unsere neue Lehre nicht anzukämpfen. Und so wird denn der Streit um sie keinen Bruno auf den Scheiterhaufen, keinen Galilei vor oder gar in die Folterkammer führen. Zumal sich ja wohl seit jener Zeit die Achtung vor fremder Überzeugung und die allgemeine Gesittung gehoben hat, wenn auch noch so viele und noch so bekannte Tatsachen beweisen, daß man seine Anforderungen in dieser Hinsicht nicht allzu hoch stellen darf.
a) Wissenschaftliche. Die grundlegenden Abhandlungen von Lorentz, Einstein, Minkowski sind bequem zugänglich in »Fortschritte der Math. Wissenschaften in Monographien«, hrsg. von O. Blumenthal. Bei Teubner Heft 1, 1910; Heft 2, 1913. M. v. Laue: »Das Relativitätsprinzip«. Braunschweig 1911. Die allgemeine Relativitätstheorie behandelt H. Weyl: »Raum, Zeit, Materie,« 3. Aufl. Berlin 1920.
b) Populäre. Wir beschränken uns auf Schriften, die über die vorliegende hinausführen: A. Einstein: »Spezielle und allgemeine Relativitätstheorie.« Sammlung Vieweg. 12. Aufl. Eine gute elementar-mathematische Einführung in die spezielle Relativitätstheorie gibt W. Bloch: »Aus Natur und Geisteswelt« (Teubner) Bd. 618. Adam Angersbach, Bd. 39 der Math.-Physik. Bibliothek (Teubner), bringt zahlreiche, sorgfältig durchgeführte Rechenbeispiele. Eine ausführliche, sehr gute Darstellung gibt: Max Born: »Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen«; Springer Berlin. – Aus der Math.-Physik. Bibliothek weisen wir auch hin auf Bd. 17: W. Brunner: »Dreht sich die Erde« und Bd. 40: Kirchberger: »Mathematische Streifzüge durch die Geschichte der Astronomie«.
Eine ganz vortreffliche Einführung in die allgemeine Relativitätstheorie gibt M. Schlick: »Raum und Zeit in der gegenwärtigen Physik«, 3. Aufl., Springer, 1920. Die »Grundlagen der Einsteinschen Gravitationstheorie« von Erwin Freundlich, 4. Aufl., Springer, 1920, sind mathematisch gehalten. Über den Zusammenhang mit geometrischen Fragen verweisen wir in erster Linie auf Arthur Haas: »Die Physik als geometrische Notwendigkeit«, »Die Naturwissenschaften« 1920 S. 121; Derselbe: »Axiomatik der modernen Physik« a. a. O. 1919 S. 744, und Helmholtz, Vorträge und Reden 2. Bd. S. 1. Braunschweig 1896. Empfohlen sei auch: A. Einstein: »Dialog über die Einwände gegen die Relativitätstheorie«, »Die Naturwissenschaften« 1918 S. 697.
c) Philosophische. Wir verweisen in erster Linie auf J. Petzoldt: »Stellung der Relativitätstheorie in der geistigen Entwicklung der Menschheit«, Dresden, Sibyllenverlag 1921. Die Schrift steht auf dem Standpunkt des Machschen Positivismus. Auf dem Standpunkt des Kantschen Systems steht Ernst Cassirer: »Zur Einsteinschen Relativitätstheorie«, Berlin 1921 (Bruno Cassirer). Ähnlich Ilse Schneider: »Das Raum-Zeitproblem bei Kant und Einstein« (Springer 1921), während Hans Reichenbach: »Relativitätstheorie und Erkenntnis a priori« auf anderm Standpunkt steht. Schließlich erwähnen wir Otto Siebert: »Albert Einsteins Relativitätstheorie und ihre kosmologischen und philosophischen Konsequenzen.« Langensalza 1921.
∞